

分析 (1)運用三角形的內角和定理求解;
(2)利用三角形的外角等于與它不相鄰的兩內角之和求解.
解答 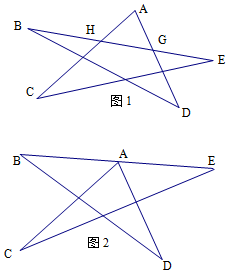 解:(1)AC與BE相交于點H,AD與BE相交于點G,
解:(1)AC與BE相交于點H,AD與BE相交于點G,
如圖,∵∠AHG是△HCE的外角,
∴∠AHG=∠C+∠E,
∵∠AGH是△GBD的外角,
∴∠AGH=∠B+∠D,
∵∠A+∠AHG+∠AGH=180,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)不變,∠CAD+∠B+∠ACE+∠D+∠E=180°.
理由:由三角形的外角性質,知∠BAC=∠E+∠ACE,∠EAD=∠B+∠D,
∴∠C+∠E+∠CAD+∠B+∠D=180°,
即∠CAD+∠B+∠C+∠D+∠E=180°.
點評 本題考查三角形外角的性質及三角形的內角和定理,解答的關鍵是溝通外角和內角的關系.


科目:初中數學 來源: 題型:選擇題
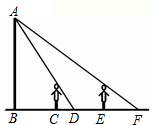 如圖一天晚上,小穎由路燈A下的B處走到C處時,測得影子CD的長為1米,當她繼續往前走到D處時,測得影子DE的長剛好是自己的身高,已知小穎的身高為1.5米,那么路燈A的高度AB為( )
如圖一天晚上,小穎由路燈A下的B處走到C處時,測得影子CD的長為1米,當她繼續往前走到D處時,測得影子DE的長剛好是自己的身高,已知小穎的身高為1.5米,那么路燈A的高度AB為( )| A. | 8米 | B. | 6米 | C. | 4.5米 | D. | 3米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
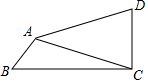 如圖,在四邊形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,則AC=$\frac{8\sqrt{10}}{5}$.
如圖,在四邊形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,則AC=$\frac{8\sqrt{10}}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
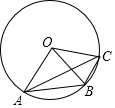 如圖,A,B,C是⊙O上三個點,∠AOB=2∠BOC,則下列說法中正確的是( )
如圖,A,B,C是⊙O上三個點,∠AOB=2∠BOC,則下列說法中正確的是( )| A. | ∠OBA=∠OCA | B. | 四邊形OABC內接于⊙O | ||
| C. | AB=2BC | D. | ∠OBA+∠BOC=90° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,正方形ABCD的邊長為2,其面積記作S1,以CD為斜邊作等腰直角三角形,以該等腰三角形的一條直角邊為邊向外作正方形,其面積記作S2,…,按照此規律繼續下去,則S2017的值為( )
如圖,正方形ABCD的邊長為2,其面積記作S1,以CD為斜邊作等腰直角三角形,以該等腰三角形的一條直角邊為邊向外作正方形,其面積記作S2,…,按照此規律繼續下去,則S2017的值為( )| A. | ($\frac{\sqrt{2}}{2}$)2014 | B. | ($\frac{1}{2}$)2014 | C. | ($\frac{\sqrt{2}}{2}$)2015 | D. | ($\frac{1}{2}$)2015 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com