
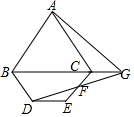
 如圖,等邊三角形ABC中,AB=3,點D是△ABC外一點,連接BD,將線段BD繞點D順時針旋轉(zhuǎn)120°得到線段DE,連接CE,點F事CE的中點,射線DF與BC邊的延長線交于點G,連接AG,若∠CBD=60°,∠ACE=90°,則線段AG的長為$\sqrt{13}$.
如圖,等邊三角形ABC中,AB=3,點D是△ABC外一點,連接BD,將線段BD繞點D順時針旋轉(zhuǎn)120°得到線段DE,連接CE,點F事CE的中點,射線DF與BC邊的延長線交于點G,連接AG,若∠CBD=60°,∠ACE=90°,則線段AG的長為$\sqrt{13}$. 分析 過A作AH⊥BC于H,延長BD,CE交于M,解直角三角形得到AH=$\frac{3\sqrt{3}}{2}$,CH=$\frac{3}{2}$,根據(jù)平行線的判定定理得到BC∥DE,由平行線的性質(zhì)得到∠EDF=∠CGF,根據(jù)全等三角形的性質(zhì)得到CG=DE,由將線段BD繞點D順時針旋轉(zhuǎn)120°得到線段DE,得到BD=DE,根據(jù)三角形的內(nèi)角和得到∠M=90°,根據(jù)平行線的性質(zhì)得到∠DEM=30°,由直角三角形的性質(zhì)得到DE=BD=2DM,根據(jù)勾股定理即可得到結(jié)論.
解答 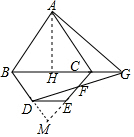 解:過A作AH⊥BC于H,延長BD,CE交于M,
解:過A作AH⊥BC于H,延長BD,CE交于M,
∵等邊三角形ABC中,AB=3,
∴AH=$\frac{3\sqrt{3}}{2}$,CH=$\frac{3}{2}$,
∵∠BDE=120°,∠CBD=60°,
∴∠BDE+∠CBD=180°,
∴BC∥DE,
∴∠EDF=∠CGF,
∵點F是CE的中點,
∴DF=CF,
在△DEF與△GCF中,$\left\{\begin{array}{l}{∠EDF=∠CGF}\\{∠DFE=∠GFC}\\{EF=CF}\end{array}\right.$,
∴△DEF≌△GCF,
∴CG=DE,
∵將線段BD繞點D順時針旋轉(zhuǎn)120°得到線段DE,
∴BD=DE,
∴BD=DE=CG,
∵∠ACE=90°,∠ACB=60°,
∴∠BCE=30°,
∴∠M=90°,
∵DE∥BC,
∴∠DEM=30°,
∴DE=BD=2DM,
∴BD=$\frac{2}{3}$BM,
∵BC=3,
∴BM=$\frac{1}{2}$BC=$\frac{3}{2}$
∴BD=1,
∴CG=1,
∴HG=2.5,
∴AG=$\sqrt{A{H}^{2}+H{G}^{2}}$=$\sqrt{13}$.
故答案為:$\sqrt{13}$.
點評 本題考查了旋轉(zhuǎn)的性質(zhì),全等三角形的判斷和性質(zhì),勾股定理,等邊三角形的性質(zhì),正確的作出輔助線是解題的關鍵.


科目:初中數(shù)學 來源: 題型:解答題
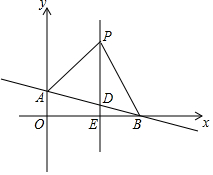 如圖,在平面直角坐標系中,直線AB:y=kx+1(k≠0)交y軸于點A,交x軸于點B(3,0),平行于y軸的直線x=2交AB于點D,交x軸于點E,點P是直線x=2上一動點,且在點D的上方,設P(2,n).
如圖,在平面直角坐標系中,直線AB:y=kx+1(k≠0)交y軸于點A,交x軸于點B(3,0),平行于y軸的直線x=2交AB于點D,交x軸于點E,點P是直線x=2上一動點,且在點D的上方,設P(2,n).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,已知正方形鐵絲框ABCD邊長為10,現(xiàn)使其變形為以A為圓心,AB為半徑的扇形(忽略鐵絲的粗細),則所得的扇形的面積為( )
如圖,已知正方形鐵絲框ABCD邊長為10,現(xiàn)使其變形為以A為圓心,AB為半徑的扇形(忽略鐵絲的粗細),則所得的扇形的面積為( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,A、B兩點分別位于一個池塘的兩端,小明想用繩子測量A,B的距離,但繩子不夠,一位同學幫他想了一個主意:先在地上取一個可以直接達到A的點C,找到AC,BC的中點D,E,并且量得DE的長為15米,則A,B兩點間的距離是( )
如圖,A、B兩點分別位于一個池塘的兩端,小明想用繩子測量A,B的距離,但繩子不夠,一位同學幫他想了一個主意:先在地上取一個可以直接達到A的點C,找到AC,BC的中點D,E,并且量得DE的長為15米,則A,B兩點間的距離是( )| A. | 15米 | B. | 20米 | C. | 30米 | D. | 40米 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖,一直線與兩坐標軸的正半軸分別交于A,B兩點,P是線段AB上任意一點(不包括端點).過點P分別作兩坐標軸的垂線,且與兩坐標軸圍成的矩形的周長為10,則該直線的函數(shù)表達式是y=-x+5.
如圖,一直線與兩坐標軸的正半軸分別交于A,B兩點,P是線段AB上任意一點(不包括端點).過點P分別作兩坐標軸的垂線,且與兩坐標軸圍成的矩形的周長為10,則該直線的函數(shù)表達式是y=-x+5.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,一次函數(shù)y1=x與二次函數(shù)y2═ax2+bx+c圖象相交于P,Q兩點,對于函數(shù)y3═ax2+(b-1)x+c,有下列結(jié)論:
如圖,一次函數(shù)y1=x與二次函數(shù)y2═ax2+bx+c圖象相交于P,Q兩點,對于函數(shù)y3═ax2+(b-1)x+c,有下列結(jié)論:| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com