
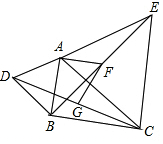
 如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點G,F(xiàn)分別是DC,BE的中點,連接AF,F(xiàn)G.
如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點G,F(xiàn)分別是DC,BE的中點,連接AF,F(xiàn)G.分析 (1)根據(jù)等式的性質(zhì)就可以得出∠DAC=∠BAE,進而得出△ADC≌△ABE,根據(jù)全等三角形的性質(zhì)就可以得出DC=BE;
(2)連接AG,根據(jù)條件就可以得出△ADG≌△ABF,根據(jù)全等三角形的性質(zhì)就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性質(zhì),就可以求出∠AFG的值;
(3)與(2)中的方法類似,根據(jù)條件得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性質(zhì),就可以表示∠AFG與α的關(guān)系.
解答 解:(1)∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE(SAS),
∴DC=BE;
(2)如圖,連接AG.
∵△ADC≌△ABE,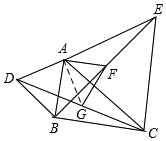
∴∠ADC=∠ABE,AD=AB.
∵G、F分別是DC與BE的中點,
∴DG=$\frac{1}{2}$DC,BF=$\frac{1}{2}$BE,
∴DG=BF.
在△ADG和△ABF中,
$\left\{\begin{array}{l}{AD=AB}\\{∠ADC=∠ABE}\\{DG=BF}\end{array}\right.$,
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG-∠BAG=∠BAF-∠BAG,
∴∠DAB=∠GAF.
∵∠DAB=80°,
∴∠GAF=80°.
∵∠GAF+∠AFG+∠AGF=180°,
∴∠AFG=$\frac{1}{2}$(180°-80°)=50°;
(3)∠AFG與α之間滿足的數(shù)量關(guān)系為:∠AFG=90°-$\frac{1}{2}$α.
由(2)可得,當∠DAB=α時,∠GAF=α.
∵∠GAF+∠AFG+∠AGF=180°,
∴α+2∠AFG=180°,
∴∠AFG=90°-$\frac{1}{2}$α.
點評 本題屬于三角形綜合題,主要考查了全等三角形的判定及性質(zhì),三角形內(nèi)角和定理以及等腰三角形的判定與性質(zhì)的綜合運用,解題時需要運用全等三角形的對應邊相等的性質(zhì),運用SAS證明三角形全等是解決問題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:解答題
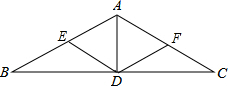 如圖,在△ABC中,AB=AC,∠BAC=120°,AD是BC邊的中線,點E、F分別是AB、AC的中點,連接DE、DF.
如圖,在△ABC中,AB=AC,∠BAC=120°,AD是BC邊的中線,點E、F分別是AB、AC的中點,連接DE、DF.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 經(jīng)過我區(qū)的濟南市第一條地鐵R1線正緊鑼密鼓施工,施工單位為了提醒司機注意繞行,在某路口設立了交通路況指示牌(如圖),已知立桿AB高度是3m,從側(cè)面D點測得顯示牌頂端C點和底端B點的仰角分別是60°和45°,求路況指示牌BC的高度(可保留根號).
經(jīng)過我區(qū)的濟南市第一條地鐵R1線正緊鑼密鼓施工,施工單位為了提醒司機注意繞行,在某路口設立了交通路況指示牌(如圖),已知立桿AB高度是3m,從側(cè)面D點測得顯示牌頂端C點和底端B點的仰角分別是60°和45°,求路況指示牌BC的高度(可保留根號).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com