

分析 (1))①證明:如圖1中,作PE⊥OA于E,PF⊥OB于F,只要證明△PEM≌△PFN(ASA),即可推出PM=PN.
②只要證明四邊形EOFP是正方形,由OP=4$\sqrt{2}$,推出OF=PF=PE=OE=4,推出正方形EOFP的面積為16,由S△PEM=S△PFN,推出四邊形PMON的面積=正方形EOFP的面積,由此即可解決問題.
解答 (1)①證明:如圖1中,作PE⊥OA于E,PF⊥OB于F,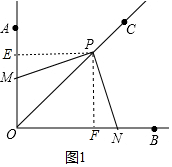
∵∠AOB=∠PEO=∠PFO=90°,
∴四邊形EOFP是矩形,
∴∠EPF=∠MPN=90°,
∴∠EPM=∠NPF,
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF,
在△PEM和△PFN中,
$\left\{\begin{array}{l}{∠PEM=∠PFN}\\{PE=PF}\\{∠EPM=∠FPN}\end{array}\right.$,
∴△PEM≌△PFN(ASA),
∴PM=PN.
②解:由①可知四邊形EOFP是矩形,
∵PE=PF,
∴四邊形EOFP是正方形,
∵OP=4$\sqrt{2}$,
∴OF=PF=PE=OE=4,
∴正方形EOFP的面積為16,
∵S△PEM=S△PFN,
∴四邊形PMON的面積=正方形EOFP的面積,
∴四邊形PMON的面積S=16,
故答案為16.
(2)解:如圖2中,結(jié)論仍然成立.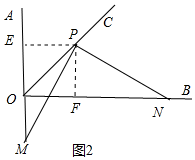
理由:∵∠AOB=∠PEO=∠PFO=90°,
∴四邊形EOFP是矩形,
∴∠EPF=∠MPN=90°,
∴∠EPM=∠NPF,
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF,
在△PEM和△PFN中,
$\left\{\begin{array}{l}{∠PEM=∠PFN}\\{PE=PF}\\{∠EPM=∠FPN}\end{array}\right.$,
∴△PEM≌△PFN(ASA),
∴PM=PN.
點評 本題考查全等三角形的判定和性質(zhì)、角平分線的性質(zhì)定理、正方形的判定和性質(zhì)等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線,構(gòu)造全等三角形解決問題,屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 平頂山市積極開展“節(jié)水”活動,小明利用課余時間對某小區(qū) 300戶居民的用 水情況進(jìn)行統(tǒng)計,發(fā)現(xiàn)12月份各戶居民的用水量比11月份有所下降,小明將12月份各戶居民的節(jié)水量統(tǒng)汁整理成如下統(tǒng)計圖表:
平頂山市積極開展“節(jié)水”活動,小明利用課余時間對某小區(qū) 300戶居民的用 水情況進(jìn)行統(tǒng)計,發(fā)現(xiàn)12月份各戶居民的用水量比11月份有所下降,小明將12月份各戶居民的節(jié)水量統(tǒng)汁整理成如下統(tǒng)計圖表:| 節(jié)水量(噸) | 1 | 1.5 | 2.5 | 3 |
| 戶數(shù) | 50 | 80 | 100 | 70 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 最少8輛 | B. | 最多8輛 | C. | 最少7輛 | D. | 最多7輛 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
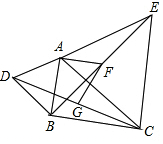 如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點G,F(xiàn)分別是DC,BE的中點,連接AF,F(xiàn)G.
如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點G,F(xiàn)分別是DC,BE的中點,連接AF,F(xiàn)G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖是一個正方體的表面展開圖,相對面上兩個數(shù)互為相反數(shù),則x+y=( )
如圖是一個正方體的表面展開圖,相對面上兩個數(shù)互為相反數(shù),則x+y=( )| A. | 6 | B. | -5 | C. | 7 | D. | -6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 2016年6月20日,新一期全球超級計算機500強榜單公布,使用中國自主芯片制造的“神威太湖之光”取代“天河二號”登上榜首,中國超算上榜總數(shù)量也有史以來首次超過美國名列第一.據(jù)國際TOP500組織當(dāng)天發(fā)布的榜單,“神威太湖之光”的浮點運算速度為每秒930000000億次,不僅速度比第二名“天河二號”快出近兩倍,其效率也提高3倍.930000000億次用科學(xué)記數(shù)法可表示為( )億次.
2016年6月20日,新一期全球超級計算機500強榜單公布,使用中國自主芯片制造的“神威太湖之光”取代“天河二號”登上榜首,中國超算上榜總數(shù)量也有史以來首次超過美國名列第一.據(jù)國際TOP500組織當(dāng)天發(fā)布的榜單,“神威太湖之光”的浮點運算速度為每秒930000000億次,不僅速度比第二名“天河二號”快出近兩倍,其效率也提高3倍.930000000億次用科學(xué)記數(shù)法可表示為( )億次.| A. | 9.3×108 | B. | 9.3×107 | C. | 93×107 | D. | 0.93×109 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com