

分析 (1)根據(jù)勾股定理求得AC=16cm,根據(jù)運(yùn)動的速度和時間求得CP=5cm,AP=11cm,最后根據(jù)勾股定理得到BP=13cm,即可得到△ABP的周長為:AP+PB+AB=44cm;
(2)根據(jù)BP=CP,則∠PCB=∠B,進(jìn)而得出PA=PB=10cm,故點(diǎn)P的運(yùn)動路程=AC+AP=26cm,最后根據(jù)t=26÷1=26s,得到當(dāng)t為26秒時,PC=PB;
(3)過點(diǎn)P作PD⊥AB于點(diǎn)D,判定Rt△BPD≌Rt△BPC(HL),得到BD=BC=12cm,AD=20-12=8cm,再設(shè)PC=xcm,則PD=xcm,AP=(16-x)cm,在Rt△APD中,根據(jù)勾股定理得到PD2+AD2=AP2,即x2+82=(16-x)2,解得x=6,即可得到當(dāng)t=6秒時,BP平分∠ABC.
解答 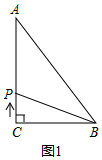 解:(1)如圖1,∵∠C=90°,AB=20cm,BC=12cm,
解:(1)如圖1,∵∠C=90°,AB=20cm,BC=12cm,
∴AC=16cm,
∵點(diǎn)P的速度為每秒1cm,
∴出發(fā)5秒時,CP=5cm,AP=11cm,
∵∠C=90°,
∴Rt△BCP中,BP=13cm,
∴△ABP的周長為:AP+PB+AB=44cm;
(2)當(dāng)點(diǎn)P在AC邊上時,PB>PC;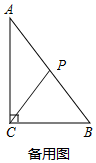
如圖,當(dāng)點(diǎn)P在AB邊上時,
若BP=CP,則∠PCB=∠B,
∵∠ACP+∠PCB=90°,∠B+∠A=90°,
∴∠ACP=∠A,
∴PA=PC,
∴PA=PB=10cm,
∴點(diǎn)P的運(yùn)動路程=AC+AP=26cm,
∴t=26÷1=26s,
∴當(dāng)t為26秒時,PC=PB;
(3)如圖,過點(diǎn)P作PD⊥AB于點(diǎn)D,
∵BP平分∠ABC,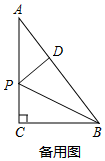
∴PD=PC,
在Rt△BPD和Rt△BPC中,
$\left\{\begin{array}{l}{BP=BP}\\{PC=PD}\end{array}\right.$,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=12cm,
∴AD=20-12=8cm,
設(shè)PC=xcm,則PD=xcm,AP=(16-x)cm,
在Rt△APD中,PD2+AD2=AP2,
即x2+82=(16-x)2,
解得x=6,
∴當(dāng)t=6秒時,BP平分∠ABC.
點(diǎn)評 本題屬于三角形綜合題,主要考查了勾股定理,等腰三角形的性質(zhì),全等三角形的判定與性質(zhì)以及角平分線的性質(zhì)的綜合應(yīng)用,解決第(3)問的關(guān)鍵是作輔助線構(gòu)造直角三角形,運(yùn)用勾股定理列出方程進(jìn)行求解.解題時注意方程思想的運(yùn)用.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5個,1個 | B. | 5個,2個 | C. | 4個,1個 | D. | 4個,2個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 最少8輛 | B. | 最多8輛 | C. | 最少7輛 | D. | 最多7輛 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
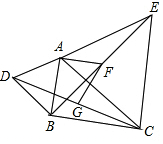 如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點(diǎn)G,F(xiàn)分別是DC,BE的中點(diǎn),連接AF,F(xiàn)G.
如圖,在△ABC中,分別以AB,AC為邊向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,連接DC,BE,點(diǎn)G,F(xiàn)分別是DC,BE的中點(diǎn),連接AF,F(xiàn)G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖是一個正方體的表面展開圖,相對面上兩個數(shù)互為相反數(shù),則x+y=( )
如圖是一個正方體的表面展開圖,相對面上兩個數(shù)互為相反數(shù),則x+y=( )| A. | 6 | B. | -5 | C. | 7 | D. | -6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,是由幾個大小相同的小正方體所搭成的幾何體從上面看到的形狀圖,小正方形中的數(shù)字表示在這個位置小正方體的個數(shù),請分別畫出從正面、左面看到的這個幾何體的形狀圖.
如圖,是由幾個大小相同的小正方體所搭成的幾何體從上面看到的形狀圖,小正方形中的數(shù)字表示在這個位置小正方體的個數(shù),請分別畫出從正面、左面看到的這個幾何體的形狀圖.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x>-1 | B. | x≥1且x≠0 | C. | x≥-1 | D. | x≥-1且x≠0 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com