
分析 先化簡題目中的式子,然后選取一個使得原分式有意義的x的值代入即可解答本題.
解答 解:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{{x^2}-2x+1}}$
=[$\frac{3x+4}{(x+1)(x-1)}-\frac{2(x+1)}{(x+1)(x-1)}$]÷$\frac{x+2}{{{x^2}-2x+1}}$
=$\frac{x+2}{(x+1)(x-1)}•\frac{{{{(x-1)}^2}}}{x+2}$
=$\frac{x-1}{x+1}$,
當x=2時,原式=$\frac{2-1}{2+1}=\frac{1}{3}$.
點評 本題考查分式的化簡求值,解答本題的關鍵是明確分式化簡求值的方法,注意x≠±1,-2.


科目:初中數學 來源: 題型:選擇題
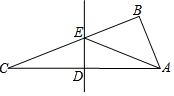 如圖,在△ABC中,∠ABC=90°,∠C=20°,DE是邊AC的垂直平分線,連結AE,則∠BAE等于( )
如圖,在△ABC中,∠ABC=90°,∠C=20°,DE是邊AC的垂直平分線,連結AE,則∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
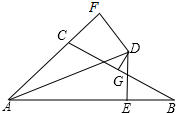 如圖∠BAC的平分線AD與BC的垂直平分線DG相交于點D,DE⊥AB,DF⊥AC,垂足分別為E,F,AB=22,AC=10,則BE=6.
如圖∠BAC的平分線AD與BC的垂直平分線DG相交于點D,DE⊥AB,DF⊥AC,垂足分別為E,F,AB=22,AC=10,則BE=6.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運輸工具 | 途中平均速度(千米/時) | 運費(元/千米) | 裝卸費(元) |
| 汽車 | 50 | 20 | 900 |
| 火車 | 100 | 15 | 2000 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com