
 正方形ABCD的邊長為1,其面積記為S1,以CD為斜邊作等腰直角三角形,以該等腰直角三角形的一條直角邊為邊向外作正方形,其面積記為S2,…按此規律繼續下去,則S9的值為( )
正方形ABCD的邊長為1,其面積記為S1,以CD為斜邊作等腰直角三角形,以該等腰直角三角形的一條直角邊為邊向外作正方形,其面積記為S2,…按此規律繼續下去,則S9的值為( )| A. | ${({\frac{1}{2}})^9}$ | B. | ${({\frac{1}{2}})^8}$ | C. | ${({\frac{{\sqrt{2}}}{2}})^9}$ | D. | ${({\frac{{\sqrt{2}}}{2}})^8}$ |
分析 根據等腰直角三角形的性質可得出S2+S2=S1,寫出部分Sn的值,根據數的變化找出變化規律Sn=($\frac{1}{2}$)n-1,依此規律即可得出結論.
解答 解:在圖中標上字母E,如圖所示.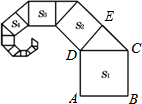
∵正方形ABCD的邊長為1,△CDE為等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
觀察,發現規律:S1=12=1,S2=$\frac{1}{2}$S1=$\frac{1}{2}$,S3=$\frac{1}{2}$S2=$\frac{1}{4}$,S4=$\frac{1}{2}$S3=$\frac{1}{8}$,…,
∴Sn=($\frac{1}{2}$)n-1.
當n=9時,S9=($\frac{1}{2}$)9-1=($\frac{1}{2}$)8,
故選:B.
點評 本題考查了等腰直角三角形的性質、勾股定理以及規律型中數的變化規律,解題的關鍵是找出規律Sn=($\frac{1}{2}$)n-1.本題屬于中檔題,難度不大,解決該題型題目時,寫出部分Sn的值,根據數值的變化找出變化規律是關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
 如圖,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一點C,延長AA1到A2,使得A1A2=A1C,在A2C上取一點D,延長A1A2到A3,使得A2A3=A2D,按此做法進行下去,∠EA3A2的度數為20°,∠A的度數為80°.
如圖,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一點C,延長AA1到A2,使得A1A2=A1C,在A2C上取一點D,延長A1A2到A3,使得A2A3=A2D,按此做法進行下去,∠EA3A2的度數為20°,∠A的度數為80°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
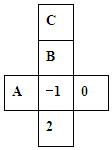 如圖是一個正方體紙盒的表面展開圖,若在其中三個正方形A、B、C內分別填入適當的數,使它折成正方體后相對的面上的兩數互為相反數,則填在正方形A、B、C內的三個數依次為( )
如圖是一個正方體紙盒的表面展開圖,若在其中三個正方形A、B、C內分別填入適當的數,使它折成正方體后相對的面上的兩數互為相反數,則填在正方形A、B、C內的三個數依次為( )| A. | -2,1,0 | B. | 1,-2,0 | C. | 0,-2,1 | D. | -2,0,1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
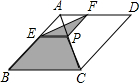 如圖所示,菱形ABCD的對角線的長分別為4和6,P是對角線AC上任一點(點P不與點A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,則陰影部分的面積是6.
如圖所示,菱形ABCD的對角線的長分別為4和6,P是對角線AC上任一點(點P不與點A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,則陰影部分的面積是6.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”
在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com