
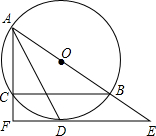
 如圖,⊙O是△ABC的外接圓,AB為直徑,∠BAC的平分線交⊙O于點(diǎn)D,過點(diǎn)D的切線分別交AB,AC的延長線于點(diǎn)E,F(xiàn)
如圖,⊙O是△ABC的外接圓,AB為直徑,∠BAC的平分線交⊙O于點(diǎn)D,過點(diǎn)D的切線分別交AB,AC的延長線于點(diǎn)E,F(xiàn)分析 (1)連接OD,如圖,利用角平分線定義得到∠1=∠2,加上∠2=∠3,則∠1=∠3,所以O(shè)D∥AF,再利用切線的性質(zhì)得OD⊥EF,于是利用平行線的性質(zhì)可得到AF⊥EF;
(2)連接OC,OD交BC于H,如圖,設(shè)CF=x,先判斷四邊形CFDH為矩形得到HD=CF=x,再證明OH為△ACB的中位線得到OH=$\frac{1}{2}$($\frac{7}{2}$-x),則利用OH=OD-DH=$\frac{5}{2}$-x得到$\frac{1}{2}$($\frac{7}{2}$-x)=$\frac{5}{2}$-x,然后解方程求出x即可.
解答 (1)證明:連接OD,如圖,
∵∠BAC的平分線交⊙O于點(diǎn)D,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,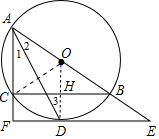
∴OD∥AF,
∵EF為切線,
∴OD⊥EF,
∴AF⊥EF;
(2)解:連接OC,OD交BC于H,如圖,設(shè)CF=x,
∵AB為直徑,
∴∠ACB=90°,
而AF⊥EF,OD⊥EF,
∴四邊形CFDH為矩形,
∴HD=CF=x,
∵OH∥AC,OA=OB,
∴OH為△ACB的中位線,
∴OH=$\frac{1}{2}$AC=$\frac{1}{2}$(AF-CF)=$\frac{1}{2}$($\frac{7}{2}$-x)
而OH=OD-DH=$\frac{5}{2}$-x,
∴$\frac{1}{2}$($\frac{7}{2}$-x)=$\frac{5}{2}$-x,解得x=$\frac{3}{2}$,
即CF的長為$\frac{3}{2}$.
點(diǎn)評(píng) 本題考查了切線的性質(zhì):圓的切線垂直于經(jīng)過切點(diǎn)的半徑.若出現(xiàn)圓的切線,必連過切點(diǎn)的半徑,構(gòu)造定理圖,得出垂直關(guān)系.也考查了圓周角定理.


 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 用小正方體搭一個(gè)幾何體,使得從上面和正面看它的圖形如圖所示.
用小正方體搭一個(gè)幾何體,使得從上面和正面看它的圖形如圖所示.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 青藏鐵路于2006年7月1日勝利通車,青藏高原天塹變通途,圓了幾代人的夢(mèng)想.作為世界上海拔最高,施工難度最大的鐵路,青藏鐵路全縣有一座大橋-拉薩河大橋(如圖)全長920多米,其中主橋長800米,小明在去年暑假乘T22次列車從北京到拉薩游玩,小明為了探究T22次列車的長度與速度,記錄了以下兩個(gè)數(shù)據(jù):
青藏鐵路于2006年7月1日勝利通車,青藏高原天塹變通途,圓了幾代人的夢(mèng)想.作為世界上海拔最高,施工難度最大的鐵路,青藏鐵路全縣有一座大橋-拉薩河大橋(如圖)全長920多米,其中主橋長800米,小明在去年暑假乘T22次列車從北京到拉薩游玩,小明為了探究T22次列車的長度與速度,記錄了以下兩個(gè)數(shù)據(jù):查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖是某住宅的平面結(jié)構(gòu)示意圖,圖中標(biāo)注了有關(guān)尺寸(墻體厚度勿略不計(jì),單位:m).
如圖是某住宅的平面結(jié)構(gòu)示意圖,圖中標(biāo)注了有關(guān)尺寸(墻體厚度勿略不計(jì),單位:m).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com