
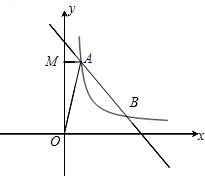
 如圖,一次函數y=mx+5的圖象與反比例函數$y=\frac{k}{x}$(k≠0)在第一象限的圖象交于A(1,n)和B(4,1)兩點,過點A作y軸的垂線,垂足為M,
如圖,一次函數y=mx+5的圖象與反比例函數$y=\frac{k}{x}$(k≠0)在第一象限的圖象交于A(1,n)和B(4,1)兩點,過點A作y軸的垂線,垂足為M,分析 (1)利用待定系數法即可解決問題.
(2)根據點A的坐標,可得OM=4,AM=1,根據S△OAM=$\frac{1}{2}$×AM×OM計算即可.
(3)如圖1中,作點A關于y軸的對稱點A′(-1,4),連接BA′交y軸于點P,此時PA+PB最小.求出直線BA′的解析式即可解決問題.
(4)分三種情形討論①QA=AB.②QB=AB.③QA=QB,分別求解即可.
(5)方程三種切線討論說明即可.
解答 解:(1)把點B(4,1)代入y=$\frac{k}{x}$得k=4,
∴反比例函數的解析式為y=$\frac{4}{x}$,
把A(1,n)代入y=$\frac{4}{x}$得n=4,
∴A(1,4),
把A(1.4)代入y=mx+5得到,m=-1,
∴一次函數的解析式為y=-x+5.
(2)∵A(1,4),AM⊥y軸,
∴AM=1,OM=4,
∴S△OAM=$\frac{1}{2}$×1×4=2.
(3)如圖1中,作點A關于y軸的對稱點A′(-1,4),連接BA′交y軸于點P,此時PA+PB最小.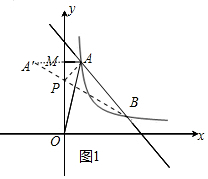
設直線BA′為y=mx+n則有$\left\{\begin{array}{l}{-k+b=4}\\{4k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=\frac{17}{5}}\end{array}\right.$,
∴直線BA′的解析式為y=-$\frac{3}{5}$x+$\frac{17}{5}$,
∴點P的坐標為(0,$\frac{17}{5}$).
(4)如圖2中,∵A(1,4),B(4,1),
∴AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
①當QA=AB時,可得Q1(0,4+$\sqrt{17}$),Q2(0,4-$\sqrt{17}$).
②當QB=AB時,可得Q3(0,1+$\sqrt{2}$),Q4(0,1-$\sqrt{2}$),
③當QA=QB時,Q5(0,0).
綜上所述,滿足條件的點Q坐標為Q1(0,4+$\sqrt{17}$),Q2(0,4-$\sqrt{17}$).Q3(0,1+$\sqrt{2}$),Q4(0,1-$\sqrt{2}$),Q5(0,0).
(5)如圖3中,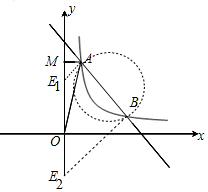
①當∠EAB=90°,可得E1(0,3).
②當∠EAB=90°,可得E2(0,-3).
③以AB為直徑的圓以y軸沒有交點,可知在y軸上不存在點E,使得E,A,B為頂點的三角形是直角三角形.
綜上所述,滿足條件的點E的坐標為(0,3)或(0,-3).
點評 本題考查反比例函數綜合題、一次函數的性質、等腰三角形的判定和性質、直角三角形的判定和性質、軸對稱最短問題等知識,解題的關鍵是靈活運用所學知識解決問題,學會用分類討論的思想思考問題,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
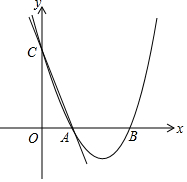 如圖所示,直線AC:y=-2x+2與x軸交于點A,與y軸交于點C,拋物線y=ax2 +bx+c(a>0)過A,C兩點,與x軸交于另一點B(B在A的右側),且△OBC∽△OCA.
如圖所示,直線AC:y=-2x+2與x軸交于點A,與y軸交于點C,拋物線y=ax2 +bx+c(a>0)過A,C兩點,與x軸交于另一點B(B在A的右側),且△OBC∽△OCA.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,AB是⊙O的切線,半徑OA=2,OB交⊙O于C,∠B=30°,則陰影部分的面積為2$\sqrt{3}$-$\frac{1}{3}$π.(結果保留π)
如圖,AB是⊙O的切線,半徑OA=2,OB交⊙O于C,∠B=30°,則陰影部分的面積為2$\sqrt{3}$-$\frac{1}{3}$π.(結果保留π)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com