
分析 (1)根據(jù)根的判別式和已知得出a-2≠0且△≥0,求出即可;
(2)根據(jù)根與系數(shù)的關(guān)系得出x1+x2=-$\frac{2a}{a-2}$,x1•x2=$\frac{a-3}{a-2}$,變形后代入,即可得出關(guān)于a的方程,求出方程的解即可.
解答 解:(1)∵關(guān)于x的一元二次方程方程(a-2)x2+2ax+a-3=0有兩個(gè)實(shí)數(shù)根,
∴a-2≠0且△≥0,
即a≠2,
△=(2a)2-4(a-2)(a-3)=20a-24≥0,
a≥$\frac{6}{5}$,
即a的取值范圍是a≥$\frac{6}{5}$且a≠2;
(2)根據(jù)根與系數(shù)的關(guān)系得:x1+x2=-$\frac{2a}{a-2}$,x1•x2=$\frac{a-3}{a-2}$,
∵${{x}_{1}}^{2}$x2+x1${{x}_{2}}^{2}$=-1,
∴x1x2(x1+x2)=-1,
∴$\frac{a-3}{a-2}$•(-$\frac{2a}{a-2}$)=-1,
解得:a=1$±\sqrt{5}$,
由(1)知:a≥$\frac{6}{5}$且a≠2,
∴a=1-$\sqrt{5}$舍去,
所以a=1+$\sqrt{5}$.
點(diǎn)評(píng) 本題考查了根的判別式和根與系數(shù)的關(guān)系等知識(shí)點(diǎn),能熟記根與系數(shù)的關(guān)系和根的判別式的內(nèi)容是解此題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
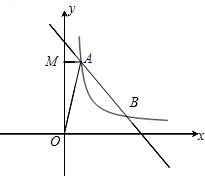 如圖,一次函數(shù)y=mx+5的圖象與反比例函數(shù)$y=\frac{k}{x}$(k≠0)在第一象限的圖象交于A(1,n)和B(4,1)兩點(diǎn),過(guò)點(diǎn)A作y軸的垂線,垂足為M,
如圖,一次函數(shù)y=mx+5的圖象與反比例函數(shù)$y=\frac{k}{x}$(k≠0)在第一象限的圖象交于A(1,n)和B(4,1)兩點(diǎn),過(guò)點(diǎn)A作y軸的垂線,垂足為M,查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 折線統(tǒng)計(jì)圖 | B. | 頻數(shù)分布直方圖 | C. | 條形統(tǒng)計(jì)圖 | D. | 扇形統(tǒng)計(jì)圖 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
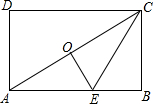 如圖,已知矩形ABCD中,點(diǎn)E在AB上,點(diǎn)O是對(duì)角線AC的中點(diǎn),沿CE折疊后,點(diǎn)B恰好與點(diǎn)O重合,若BC=6,則折痕CE的長(zhǎng)為( )
如圖,已知矩形ABCD中,點(diǎn)E在AB上,點(diǎn)O是對(duì)角線AC的中點(diǎn),沿CE折疊后,點(diǎn)B恰好與點(diǎn)O重合,若BC=6,則折痕CE的長(zhǎng)為( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com