
 E、F在菱形ABCD的邊AB和BC上,DE=DF=AD,且∠EDF=30°,則∠BEF=35°.
E、F在菱形ABCD的邊AB和BC上,DE=DF=AD,且∠EDF=30°,則∠BEF=35°. 分析 由菱形的性質得出AB=BC=CD=AD,∠A=∠C,AD∥BC,證出AD=DE=DF=CD,與等腰三角形的性質得出∠DEF=∠EFD=75°,∠A=∠DEA,∠C=∠DFC,得出∠A=∠DEA=∠C=∠DFC,由AAS證明△DAE≌△DCF,得出AE=CF,證出BE=BF,得出∠BEF=∠BFE,設∠BEF=∠BFE=x,∴∠EBF=180°-2x,∠A=∠DEA=180°-∠DEF-∠BEF=105°-x,由平行線的性質得出105°-x+180°-2x=180°,解方程即可.
解答 解:∵四邊形ABCD為菱形,
∴AB=BC=CD=AD,∠A=∠C,AD∥BC,
∵DE=DF=AD,∠EDF=30°,
∴AD=DE=DF=CD,∠DEF=∠EFD=75°,
∴∠A=∠DEA,∠C=∠DFC,
∴∠A=∠DEA=∠C=∠DFC,
在△DAE和△DCF中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠DEA=∠DFC}&{\;}\\{AD=CD}&{\;}\end{array}\right.$,
∴△DAE≌△DCF(AAS),
∴AE=CF,
∴BE=BF,
∴∠BEF=∠BFE,
設∠BEF=∠BFE=x,
∴∠EBF=180°-2x,∠A=∠DEA=180°-∠DEF-∠BEF=105°-x,
∵AD∥BC,
∴∠A+∠EBF=180°,
∴105°-x+180°-2x=180°,
解得:x=35°;
故答案為:35°.
點評 本題考查了菱形的性質、等腰三角形的性質、全等三角形的判定與性質、三角形內角和定理等知識;熟練掌握菱形的性質和等腰三角形的性質是解決問題的關鍵.


科目:初中數(shù)學 來源: 題型:選擇題

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
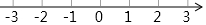 解不等式組$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并將其解集在數(shù)軸上表示出來.
解不等式組$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并將其解集在數(shù)軸上表示出來.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
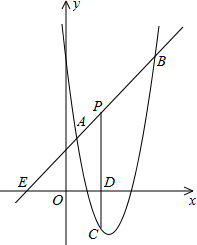 如圖,直線y=x+2與拋物線y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),點P是線段AB上異于A、B的動點,過點P作PC⊥x軸于點D,交拋物線于點C.
如圖,直線y=x+2與拋物線y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),點P是線段AB上異于A、B的動點,過點P作PC⊥x軸于點D,交拋物線于點C.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com