
| A. | $\frac{9}{4}π$ | B. | $\frac{9}{2}π$ | C. | 2π | D. | 3π |
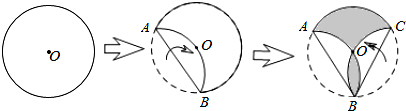
分析 作OD⊥AB于點D,連接AO,BO,CO,求出∠OAD=30°,得到∠AOB=2∠AOD=120°,進而求得∠AOC=120°,再利用陰影部分的面積=S扇形AOC求解.
解答 解;如圖,作OD⊥AB于點D,連接AO,BO,CO,
∵OD=$\frac{1}{2}$AO,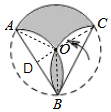
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴陰影部分的面積=S扇形AOC=$\frac{120π×{3}^{2}}{360}$=3π,
故選:C.
點評 本題考查的是扇形面積的計算、翻轉變換的性質,掌握扇形的面積公式:S=$\frac{nπ{R}^{2}}{360}$是解題的關鍵.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′為AC延長線上一點,A′是B′B延長線上一點,且△A′B′C≌△ABC,則∠BCA′:∠BCB′=1:4.
如圖,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′為AC延長線上一點,A′是B′B延長線上一點,且△A′B′C≌△ABC,則∠BCA′:∠BCB′=1:4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
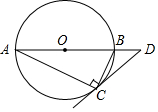 如圖,⊙O是Rt△ABC的外接圓,∠ACB=90°,∠A=25°,過點C作⊙O的切線,交AB的延長線于點D,則∠D的度數是( )
如圖,⊙O是Rt△ABC的外接圓,∠ACB=90°,∠A=25°,過點C作⊙O的切線,交AB的延長線于點D,則∠D的度數是( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某水果銷售店在試銷售成本為每千克2元的某種水果,規定試銷期間銷售單價不低于成本單價,也不高于每千克4元.經試銷發現,每天的銷售量y(千克)與銷售單價x(元)符合一次函數關系,如圖是y與x的函數關系圖象.
某水果銷售店在試銷售成本為每千克2元的某種水果,規定試銷期間銷售單價不低于成本單價,也不高于每千克4元.經試銷發現,每天的銷售量y(千克)與銷售單價x(元)符合一次函數關系,如圖是y與x的函數關系圖象.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com