
 如圖拋物線y=ax2+bx+c與x軸交于A、B兩點,其中B點坐標為(4,0),直線DE是拋物線的對稱軸,且與x軸交于點E,CD⊥DE于D,現有下列結論:
如圖拋物線y=ax2+bx+c與x軸交于A、B兩點,其中B點坐標為(4,0),直線DE是拋物線的對稱軸,且與x軸交于點E,CD⊥DE于D,現有下列結論:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①② |
分析 ①由拋物線開口向下即可得出a<0,①成立;②由拋物的對稱軸x=-$\frac{b}{2a}$>0結合a<0即可得出b>0,②不成立;③由拋物線與x軸有兩個交點即可得出b2-4ac>0,③成立;④由拋物線的對稱性可得出AE=BE,結合點B的坐標以及OE=CD即可得出AE+CD=4,④成立.綜上即可得出結論.
解答 解:①∵拋物線開口向下,
∴a<0,①成立;
②∵拋物線的對稱軸為x=-$\frac{b}{2a}$>0,
∴b>0,②不成立;
③∵拋物線與x軸有兩個交點,
∴b2-4ac>0,③成立;
④∵DE為拋物線的對稱軸,
∴AE=BE.
∵B點坐標為(4,0),
∴OB=OE+BE=CD+AE=4,④成立.
故選C.
點評 本題考查了拋物線與x軸的交點以及二次函數圖象與系數的關系,結合二次函數圖象逐一分析四條結論是否成立是解題的關鍵.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:初中數學 來源: 題型:選擇題

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
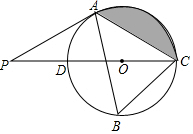 如圖,在⊙O的內接三角形ABC中,∠ABC=60°,AC=5,過點A作⊙O的切線交直徑CD的延長線于點P.
如圖,在⊙O的內接三角形ABC中,∠ABC=60°,AC=5,過點A作⊙O的切線交直徑CD的延長線于點P.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{480}{x-4}$-$\frac{480}{x}$=4 | B. | $\frac{480}{x}$-$\frac{480}{x+4}$=20 | C. | $\frac{480}{x-20}$-$\frac{480}{x}$=4 | D. | $\frac{480}{x}$-$\frac{480}{x+20}$=4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)試幫助考古人員“修補”這個破碎的圓盤(保留作圖痕跡,并寫出作法)
(1)試幫助考古人員“修補”這個破碎的圓盤(保留作圖痕跡,并寫出作法)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com