
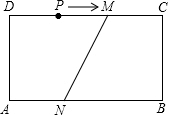
 如圖,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.點(diǎn)P在CD邊上.
如圖,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.點(diǎn)P在CD邊上.分析 (1)因?yàn)樗倪呅蜛BCD為矩形,則∠A=∠B=90°,所以點(diǎn)P一個(gè)與D重合,一個(gè)與C重合;還有兩個(gè)與AB構(gòu)建∠APB=90°,通過(guò)證明△AEP∽△PEB,可以確定P的位置,所以一共有符合條件的P點(diǎn)4個(gè);
(2)無(wú)論直線l在任一符合條件的位置上,都存在兩個(gè)H點(diǎn),構(gòu)成∠HNM=∠HMN=90°;以MN為直徑作一輔助圓O,因?yàn)橹睆剿鶎?duì)的圓周角為直角,所以首先計(jì)算當(dāng)直線l與圓O相切時(shí),PD的長(zhǎng),先計(jì)算FN=1,所以此時(shí)PD=5-1=4,如圖4,因此可以分為以下幾種情況討論:
當(dāng)0≤t<4時(shí),如圖5,有2個(gè)H點(diǎn); 當(dāng)t=4時(shí),如圖6,有3個(gè)H點(diǎn);當(dāng)4<t<5時(shí),如圖7,有4個(gè)H點(diǎn); 當(dāng)t=5時(shí),如圖8,有2個(gè)H點(diǎn);當(dāng)5<t<8時(shí),如圖9,有4個(gè)H點(diǎn);
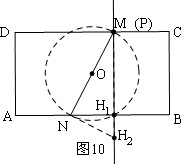
當(dāng)t=8時(shí),如圖10,有2個(gè)H點(diǎn).
解答 解:(1)①如圖1,當(dāng)∠PAB=90°時(shí),P與D重合;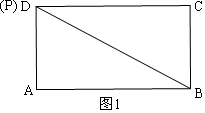
②如圖2,當(dāng)∠PBA=90°時(shí),P與C重合;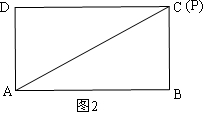
③如圖3,當(dāng)∠APB=90°時(shí),過(guò)P作PE⊥AB于E,則PE=BC=4,
設(shè)PD=x,則AE=x,EB=12-x,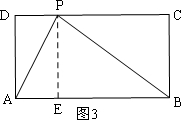
∵∠APB=90°,
∴∠APE+∠BPE=90°,
∵∠AEP=∠PEB=90°,
∴∠APE+∠PAB=90°,
∴∠BPE=∠PAB,
∴△AEP∽△PEB,
∴$\frac{AE}{PE}=\frac{PE}{EB}$,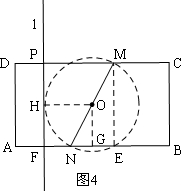
∴42=x(12-x),
x=6$±2\sqrt{5}$,
即當(dāng)PD=6$+2\sqrt{5}$和6-2$\sqrt{5}$時(shí)滿(mǎn)足∠APB=90°,
此時(shí)存在兩個(gè)符合條件的點(diǎn)P,
綜上所述,如果點(diǎn)P能與點(diǎn)A、B構(gòu)成一個(gè)直角三角形,則這樣的點(diǎn)P有4個(gè);
故答案為:4;
(2)如圖4,以MN為直徑作圓O,當(dāng)直線l為⊙O的切線時(shí),設(shè)切點(diǎn)為H,連接OH,設(shè)⊙O與AB的另一個(gè)交點(diǎn)為E,連接ME,
過(guò)O作OG⊥AB于G,
∵M(jìn)N是⊙O的直徑,
∴∠MEN=90°,
∵l∥BC,
∴l(xiāng)⊥CD,l⊥AB,
∴∠CPF=∠PFE=90°,
∴四邊形PFEM是矩形,
∴PM=EF,
∵DM=8,AN=5,
∴EN=8-5=3,
∵EM=4,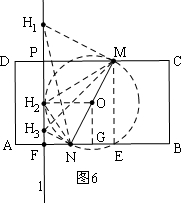
由勾股定理得:MN=5,
∵OG⊥EN,
∴NG=$\frac{1}{2}$EN=$\frac{3}{2}$,
∵l是⊙O的切線,
∴OH⊥l,
同理得:四邊形OGFH是矩形,
∴OH=FG=2.5,
∴FN=FG-NG=2.5-1.5=1;
①當(dāng)0≤t<4時(shí),如圖5,有2個(gè)H點(diǎn);
②當(dāng)t=4時(shí),如圖6,有3個(gè)H點(diǎn);
③當(dāng)4<t<5時(shí),如圖7,有4個(gè)H點(diǎn); 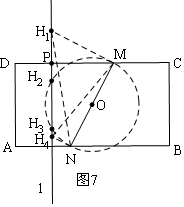
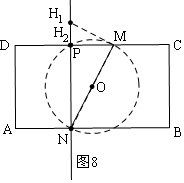
④當(dāng)t=5時(shí),如圖8,有2個(gè)H點(diǎn);
⑤當(dāng)5<t<8時(shí),如圖9,有4個(gè)H點(diǎn);
⑥當(dāng)t=8時(shí),如圖10,有2個(gè)H點(diǎn).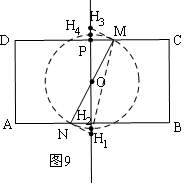
綜上所述,當(dāng)0≤t<4或t=5或t=8時(shí),有2個(gè)H點(diǎn);當(dāng)t=4時(shí),有3個(gè)H點(diǎn);當(dāng)4<t<5或5<t<8時(shí),有4個(gè)H點(diǎn).
點(diǎn)評(píng) 本題是四邊形和圓的綜合題,考查了矩形的性質(zhì)和判定、圓周角定理、垂徑定理、切線的性質(zhì)等知識(shí),有難度,尤其是第2問(wèn),解決的關(guān)鍵是構(gòu)建輔助圓,計(jì)算直線和圓相切時(shí),PD的長(zhǎng),根據(jù)這個(gè)長(zhǎng)度分情況進(jìn)行討論,要不重不漏.


 優(yōu)學(xué)名師名題系列答案
優(yōu)學(xué)名師名題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
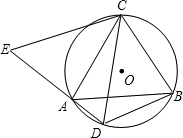 如圖,△ABC是⊙O的內(nèi)接三角形,AC=BC,D為⊙O中$\widehat{AB}$上一點(diǎn),延長(zhǎng)DA至點(diǎn)E,使CE=CD.
如圖,△ABC是⊙O的內(nèi)接三角形,AC=BC,D為⊙O中$\widehat{AB}$上一點(diǎn),延長(zhǎng)DA至點(diǎn)E,使CE=CD.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
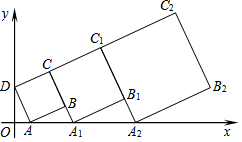 在平面直角坐標(biāo)系中,正方形ABCD的位置如下圖所示,點(diǎn)A的坐標(biāo)為(1,0),點(diǎn)D的坐標(biāo)為(0,3).延長(zhǎng)CB交x軸于點(diǎn)A1,作正方形A1B1C1C;延長(zhǎng)C1B1交x軸于點(diǎn)A2,作正方形A2B2C2C1…按這樣的規(guī)律進(jìn)行下去,第2012個(gè)正方形的面積為( )
在平面直角坐標(biāo)系中,正方形ABCD的位置如下圖所示,點(diǎn)A的坐標(biāo)為(1,0),點(diǎn)D的坐標(biāo)為(0,3).延長(zhǎng)CB交x軸于點(diǎn)A1,作正方形A1B1C1C;延長(zhǎng)C1B1交x軸于點(diǎn)A2,作正方形A2B2C2C1…按這樣的規(guī)律進(jìn)行下去,第2012個(gè)正方形的面積為( )| A. | $\sqrt{10}$×($\frac{4}{3}$)4022 | B. | 10×($\frac{4}{3}$)4022 | C. | 5×($\frac{4}{3}$)4022 | D. | 10×($\frac{4}{3}$)4023 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
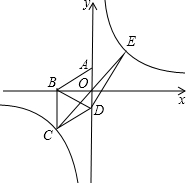 如圖,在平面直角坐標(biāo)系中四邊形ABCD為菱形,邊AD在y軸上.其中A(0,1),B(-$\sqrt{3}$,0),雙曲線y=$\frac{m}{x}$經(jīng)過(guò)點(diǎn)C.
如圖,在平面直角坐標(biāo)系中四邊形ABCD為菱形,邊AD在y軸上.其中A(0,1),B(-$\sqrt{3}$,0),雙曲線y=$\frac{m}{x}$經(jīng)過(guò)點(diǎn)C.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com