
分析 分類討論:當BE=BC時,如圖1,利用sin∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$可得到∠AEB=30°;當CE=CB,如圖2,同樣方法可得∠CED=30°,再利用AD∥BC得到∠BCE=30°,∠CBE=∠AEB,接著根據等腰三角形的性質和三角形內角和得到∠CBE=75°,于是得到∠AEB=75°,綜上所述,∠AEB的度數為30°或75°.
解答 解:當BE=BC時,如圖1,
∵四邊形ABCD為矩形,
∴BC=AD=2AB,∠A=90°,
∴BE=2AB,
在Rt△ABE中,∵sin∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$,
∴∠AEB=30°;
當CE=CB,如圖2,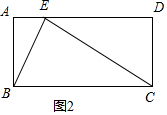
同樣可得∠CED=30°,
∵AD∥BC,
∴∠BCE=30°,∠CBE=∠AEB,
∵CE=CB,
∴∠CBE=∠CEB,
∴∠CBE=$\frac{1}{2}$(180°-30°)=75°,
∴∠AEB=75°,
綜上所述,∠AEB的度數為30°或75°.
故答案為30°或75°.
點評 本題考查了矩形的性質:平行四邊形的性質矩形都具有;矩形的四個角都是直角.也考查了等腰三角形的性質.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:解答題
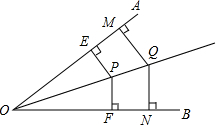 如圖,P是∠AOB內部的一點,PE⊥OA,PF⊥OB垂足分別為E,F.PE=PF.Q是OP上的任意一點,QM⊥OA,QN⊥OB,垂足分別為點M和N,QM與QN相等嗎?請證明.
如圖,P是∠AOB內部的一點,PE⊥OA,PF⊥OB垂足分別為E,F.PE=PF.Q是OP上的任意一點,QM⊥OA,QN⊥OB,垂足分別為點M和N,QM與QN相等嗎?請證明.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
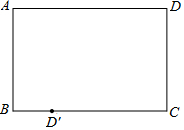 折紙:有一張矩形紙片ABCD(如圖所示),要將點D沿某條直線翻折180°,恰好落在BC邊上的點D′處,請在圖中用尺規作出該直線.(保留作圖痕跡)
折紙:有一張矩形紙片ABCD(如圖所示),要將點D沿某條直線翻折180°,恰好落在BC邊上的點D′處,請在圖中用尺規作出該直線.(保留作圖痕跡)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在△ABC中,AD是高,E是AD的中點,連接CE,并延長交AB于點P,過點A作AQ∥BC,交CP的延長線于點Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中點,連接CE,并延長交AB于點P,過點A作AQ∥BC,交CP的延長線于點Q,BD:CD:AD=1:2:3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com