

分析 (1)根據(jù)“共相似點”的定義容易得出結(jié)論.
(2)根據(jù)題意得:△ABP∽△ACB,由相似三角形的性質(zhì)得出∠ABP=∠C,同理得:∠CBP=∠A,得出∠ABC=∠A+∠C=180°-∠ABC,求出∠ABC=90°即可;
(3)根據(jù)題意得:△PBC∽△CAB,由相似三角形的性質(zhì)得出∠PBC=∠A,∠PCB=∠ABC,再由角平分線角平分線定義得出∠A=∠ABE=∠PBC,證出△BEC∽△ABC,得出點E是△ABC的邊共相似點;由直角三角形的性質(zhì)得出∠PCB+∠ABC=90°,得出2∠A+2∠A=90°,求出∠A=22.5°;
(4)通過作圖得出△ABC的“共相似點”共有8個,根據(jù)等邊三角形的性質(zhì)和直角三角形的性質(zhì)得:順次連接所有滿足條件的P點而圍成的多邊形的周長為6+$\sqrt{3}$.
解答 解:(1)根據(jù)“共相似點”的定義得:等邊三角形不存在共相似點.
故答案為:不存在;
(2)△ABC是直角三角形,理由如下:
根據(jù)題意得:△ABP∽△ACB,
∴∠ABP=∠C,
同理得:∠CBP=∠A,
∴∠ABC=∠A+∠C=180°-∠ABC,
解得:∠ABC=90°,
∴△ABC是直角三角形;
(3)根據(jù)題意得:△PBC∽△CAB,
∴∠PBC=∠A,∠PCB=∠ABC,
∵BE平分∠ABC,
∴∠ABE=∠PBC,
∴∠A=∠ABE=∠PBC,
∴∠PCB=∠ABC=2∠A=2∠PBC,
∵∠BCE=∠ACB,∠PBC=∠A,
∴△BEC∽△ABC,
∴點E是△ABC的邊共相似點;
∵CD是△ABC的高,
∴∠CDB=90°,
∴∠PCB+∠ABC=90°,
∴2∠A+2∠A=90°,
解得:∠A=22.5°;
(4)作CP⊥AB于P,則P為△ABC的“共相似點”;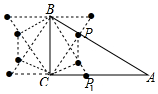
過B作BC的垂線與CP的延長線的交點是△ABC的“共相似點”;
作∠ABC的平分線與AC的交點P1是△ABC的“共相似點”;
過C作BP1的垂線,垂足是△ABC的“共相似點”;
同理:以上四個△ABC的“共相似點”關(guān)于直線BC的對稱點是△ABC的“共相似點”;
∴△ABC的“共相似點”共有8個,如圖所示:
根據(jù)等邊三角形的性質(zhì)和直角三角形的性質(zhì)得:順次連接所有滿足條件的P點而圍成的多邊形的周長為 2×2+4×$\frac{1}{2}$+2×$\frac{\sqrt{3}}{2}$=6+$\sqrt{3}$;
故答案為:8;6+$\sqrt{3}$.
點評 本題是相似形綜合題目,考查了相似三角形的判定與性質(zhì)、直角三角形的性質(zhì)等知識;理解“共相似點”定義,證明三角形相似是解決問題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 小明的手機(jī)沒電了,現(xiàn)有一個只含A,B,C,D四個同型號插座的插線板(如圖,假設(shè)每個插座都適合所有的充電插頭,且被選中的可能性相同),請計算:
小明的手機(jī)沒電了,現(xiàn)有一個只含A,B,C,D四個同型號插座的插線板(如圖,假設(shè)每個插座都適合所有的充電插頭,且被選中的可能性相同),請計算:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
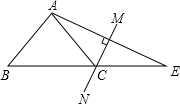 如圖,在△ABE中,∠A=108°,AE的垂直平分線MN交BE于點C,且AB=CE,則∠B的度數(shù)是( )
如圖,在△ABE中,∠A=108°,AE的垂直平分線MN交BE于點C,且AB=CE,則∠B的度數(shù)是( )| A. | 45° | B. | 48° | C. | 50° | D. | 72° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
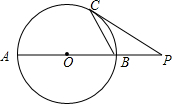 如圖,在⊙O中,AB為直徑,C為⊙O上一點,過點C作⊙O的切線,與AB的延長線相交于點P,若∠CAB=27°,求∠P的大小.
如圖,在⊙O中,AB為直徑,C為⊙O上一點,過點C作⊙O的切線,與AB的延長線相交于點P,若∠CAB=27°,求∠P的大小.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com