
分析 首先根據勾股定理求得該直角三角形的斜邊是5,再根據其外接圓的半徑等于斜邊的一半和內切圓的半徑等于兩條直角邊的和與斜邊的差的一半進行計算.
解答 解:∵直角三角形兩直角邊為3,4,
∴斜邊長=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴外接圓半徑=$\frac{5}{2}$=2.5,內切圓半徑=$\frac{3+4-5}{2}$=1,
∴外接圓和內切圓半徑之和=2.5+1=3.5.
故答案為:3.5.
點評 本題考查的是三角形的內切圓與內心,此題要熟記直角三角形外接圓的半徑和內切圓的半徑公式:外接圓的半徑等于斜邊的一半;內切圓的半徑等于兩條直角邊的和與斜邊的差的一半.


科目:初中數學 來源: 題型:解答題
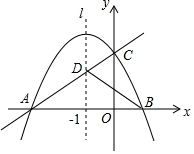 如圖,已知拋物線y=ax2+bx+c(a<0,c>0)與x軸交于A,B兩點,與y軸交于點C,其對稱軸l為x=-1,直線y=kx+m經過A,C兩點,與拋物線的對稱軸l交于點D,且AD=2CD,連接BC,BD.
如圖,已知拋物線y=ax2+bx+c(a<0,c>0)與x軸交于A,B兩點,與y軸交于點C,其對稱軸l為x=-1,直線y=kx+m經過A,C兩點,與拋物線的對稱軸l交于點D,且AD=2CD,連接BC,BD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
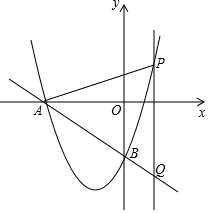 如圖,已知直線l:y=-$\frac{3}{4}$x-3與x軸交于點A,與y軸交于點B,拋物線y=ax2+bx+c經過A、B兩點,且對稱軸為直線x=-$\frac{3}{2}$.
如圖,已知直線l:y=-$\frac{3}{4}$x-3與x軸交于點A,與y軸交于點B,拋物線y=ax2+bx+c經過A、B兩點,且對稱軸為直線x=-$\frac{3}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com