
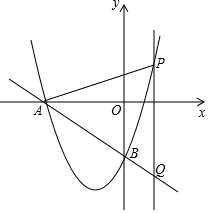
 如圖,已知直線l:y=-$\frac{3}{4}$x-3與x軸交于點A,與y軸交于點B,拋物線y=ax2+bx+c經過A、B兩點,且對稱軸為直線x=-$\frac{3}{2}$.
如圖,已知直線l:y=-$\frac{3}{4}$x-3與x軸交于點A,與y軸交于點B,拋物線y=ax2+bx+c經過A、B兩點,且對稱軸為直線x=-$\frac{3}{2}$.分析 (1)求出A、B兩點坐標,構建方程組即可解決問題.
(2)①設Q的坐標為:(x,-$\frac{3}{4}$x-3),由A(-4,0),B(0,-3),推出AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,AB的中點坐標為(-2,-$\frac{3}{2}$),因為以AB為直徑的圓恰好與直線PQ相切,可得|x-(-2)|=$\frac{5}{2}$,解方程即可解決問題.
②分三種情形,分別構建方程即可解決問題.
解答 解:(1)∵直線l:y=-$\frac{3}{4}$x-3與x軸交于點A,與y軸交于點B,
∴A(-4,0),B(0,-3),
∵拋物線y=ax2+bx+c經過A、B兩點,且對稱軸為直線x=-$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{16a-4b+c=0}\\{c=-3}\\{-\frac{b}{2a}=-\frac{3}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=\frac{9}{4}}\\{c=-3}\end{array}\right.$,
∴拋物線的解析式為:y=$\frac{3}{4}$x2+$\frac{9}{4}$x-3;
(2)①設Q的坐標為:(x,-$\frac{3}{4}$x-3),
∵A(-4,0),B(0,-3),
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,AB的中點坐標為(-2,-$\frac{3}{2}$),
∵以AB為直徑的圓恰好與直線PQ相切,
∴|x-(-2)|=$\frac{5}{2}$,
解得:x=$\frac{1}{2}$或-$\frac{9}{2}$,
∴此時點Q的坐標為:($\frac{1}{2}$,-$\frac{27}{8}$)或(-$\frac{9}{2}$,$\frac{3}{8}$);
②設P的坐標為(x,$\frac{3}{4}$x2+$\frac{9}{4}$x-3),則Q(x,-$\frac{3}{4}x-3$)
如圖1中,當PA=PQ時,作PM⊥AQ于M,設PQ交x軸于N.易知PQ=$\frac{3}{4}$x2+3x,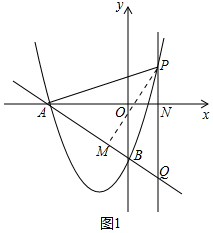
∵OB∥NQ,
∴OA:AN=AB:AQ,
∴4:(4+x)=5:AQ,
∴AQ=$\frac{5}{4}$(4+x),AM=MQ=$\frac{5}{8}$(4+x),
∵cos∠AQN=cos∠PQM=$\frac{3}{5}$,
∴$\frac{\frac{5}{8}(4+x)}{\frac{3}{4}{x}^{2}+3x}=\frac{3}{5}$,
解得x=$\frac{25}{18}$或-4(舍棄),此時Q($\frac{25}{18}$,-$\frac{97}{24}$).
如圖2中,當QA=QP時,則有$\frac{5}{4}$(4+x)=$\frac{3}{4}$x2+3x,解得x=$\frac{5}{3}$或-4(舍棄),此時Q($\frac{5}{3}$,-$\frac{17}{4}$).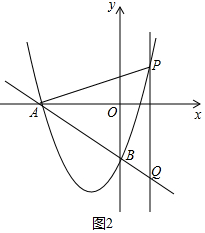
如圖3中,當AP=AQ時,設AP交y軸于N.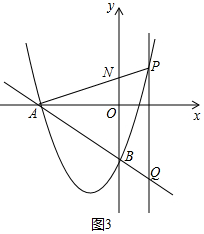
∵直線AP與直線AQ關于x軸對稱,
∴N(0,3),
∴直線AN的解析式為y=$\frac{3}{4}$x+3,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x+3}\\{y=\frac{3}{4}{x}^{2}+\frac{9}{4}x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=\frac{9}{2}}\end{array}\right.$,
∵A(-4,0),
∴P(2,$\frac{9}{2}$),
∴Q(2,-$\frac{9}{2}$),
綜上所述,滿足條件的點Q的坐標為($\frac{25}{18}$,-$\frac{97}{24}$)或($\frac{5}{3}$,-$\frac{17}{4}$)或(2,-$\frac{9}{2}$).
點評 本題考查二次函數綜合題、待定系數法、等腰三角形的判定和性質、一元二次方程等知識,解題的關鍵是靈活運用所學知識,學會用分類討論的思想思考問題,學會構建方程解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
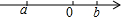 在數軸上實數a,b的位置如圖所示,化簡|a+b|+$\sqrt{(a-b)^{2}}$的結果是( )
在數軸上實數a,b的位置如圖所示,化簡|a+b|+$\sqrt{(a-b)^{2}}$的結果是( )| A. | -2a-b | B. | -2a+b | C. | -2b | D. | -2a |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com