
分析 (1)根據菱形的性質可得出AB=AD,由根的判別式即可得出關于m的一元二次方程,解之即可得出m的值;
(2)將x=2代入一元二次方程可求出m的值,再根據根與系數的關系即可得出AB+AD的值,利用平行四邊形的性質即可求出平行四邊形ABCD的周長.
解答 解:(1)∵四邊形ABCD是菱形,
∴AB=AD,
∵AB、AD的長是關于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的兩個實數根,
∴△=(-m)2-4($\frac{m}{2}$-$\frac{1}{4}$)=m2-2m+1=0,
解得:m=1.
∴當m為1時,四邊形ABCD是菱形.
(2)將x=2代入x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0中,得:4-2m+$\frac{m}{2}$-$\frac{1}{4}$=0,
解得:m=$\frac{5}{2}$,
∵AB、AD的長是關于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的兩個實數根,
∴AB+AD=m=$\frac{5}{2}$,
∴平行四邊形ABCD的周長=2(AB+AD)=2×$\frac{5}{2}$=5.
點評 本題考查了根的判別式、菱形的性質、平行四邊形的性質以及根與系數的關系,解題的關鍵是:(1)根據根的判別式找出關于m的一元二次方程;(2)將x=2代入原方程求出m值.


科目:初中數學 來源: 題型:解答題
 在平面直角坐標系上畫出y=2x-2的圖象
在平面直角坐標系上畫出y=2x-2的圖象查看答案和解析>>
科目:初中數學 來源: 題型:解答題
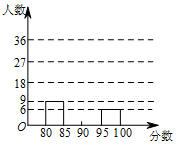 為活躍校園生活,某校開展了“我歌唱我快樂”海選比賽活動,抽取海選中部分參賽同學的成績分別繪制成頻數分布表和頻數分布直方圖(均不完整)如下:
為活躍校園生活,某校開展了“我歌唱我快樂”海選比賽活動,抽取海選中部分參賽同學的成績分別繪制成頻數分布表和頻數分布直方圖(均不完整)如下:| 分數段 | 頻數 | 頻率 |
| 80≤x<85 | 9 | 0.15 |
| 85≤x<90 | m | 0.45 |
| 90≤x<95 | ■ | ■ |
| 95≤x<100 | 6 | n |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知A、B兩地相距80km,甲、乙兩人沿同一條道路從A地到B地,l1,l2分別表示甲、乙兩人離開A地的距離s(km)與時間t(h)之間的關系.
已知A、B兩地相距80km,甲、乙兩人沿同一條道路從A地到B地,l1,l2分別表示甲、乙兩人離開A地的距離s(km)與時間t(h)之間的關系.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com