
分析 (1)總費用=0.6×A型車廂節數+0.8×B型車廂節數.
(2)應分別表示出兩類車廂能裝載的甲乙兩種貨物的質量.35×A型車廂節數+25×B型車廂節數≥1240;15×A型車廂節數+35×B型車廂節數≥880.
(3)應結合(1)的函數,(2)的自變量的取值來解決.
解答 解:(1)6000元=0.6萬元,8000元=0.8萬元,
設用A型車廂x節,則用B型車廂(40-x)節,總運費為y萬元,
依題意,得y=0.6x+0.8(40-x)=-0.2x+32;
(2)依題意,得$\left\{\begin{array}{l}{35x+25(40-x)≥1240}\\{15x+35(40-x)≥880}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x≥24}\\{x≤26}\end{array}\right.$,
∴24≤x≤26,
∵x取整數,故A型車廂可用24節或25節或26節,相應有三種裝車方案:
①24節A型車廂和16節B型車廂;
②25節A型車廂和15節B型車廂;
③26節A型車廂和14節B型車廂.
(3)由函數y=-0.2x+32知,x越大,y越少,故當x=26時,運費最省,這時y=-0.2×26+32=26.8(萬元),
答:安排A型車廂26節、B型車廂14節運費最省,最小運費為26.8萬元.
點評 此題考查了一次函數的應用,解決本題的關鍵是讀懂題意,找到所求量的等量關系及符合題意的不等關系式組.


科目:初中數學 來源: 題型:選擇題
 如圖所示,AD平分∠BAC,AB=AC,連結BD、CD并延長分別交AC、AB于F、E點,則此圖中全等三角形的對數為( )
如圖所示,AD平分∠BAC,AB=AC,連結BD、CD并延長分別交AC、AB于F、E點,則此圖中全等三角形的對數為( )| A. | 2對 | B. | 3對 | C. | 4對 | D. | 5對 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
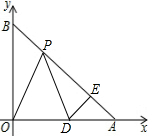 已知在平面直角坐標系中,A(a,0)、B(0,b)滿足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是線段AB上一動點,D是x軸正半軸上一點,且PO=PD,DE⊥AB于E.
已知在平面直角坐標系中,A(a,0)、B(0,b)滿足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是線段AB上一動點,D是x軸正半軸上一點,且PO=PD,DE⊥AB于E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 為了測量校園內旗桿的高度,小強先將升旗的繩子拉直到旗桿底端,并在與旗桿低端齊平的繩子處做好標記,測得剩余繩子的長度為0.5米,然后將繩子低端拉至離旗桿底端3.5米處(繩子被拉直且低端恰好與地面接觸).請你算出旗桿的高度.
為了測量校園內旗桿的高度,小強先將升旗的繩子拉直到旗桿底端,并在與旗桿低端齊平的繩子處做好標記,測得剩余繩子的長度為0.5米,然后將繩子低端拉至離旗桿底端3.5米處(繩子被拉直且低端恰好與地面接觸).請你算出旗桿的高度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com