

分析 (1)先根據等腰直角三角形的性質,得出△AED≌△CFD(SAS),進而得到DE=DF,∠ADE=∠CDF,再根據CD⊥AB,即可推導得出∠EDF=90°,進而得到△DEF是等腰直角三角形;
(2)①先根據△DEF是等腰直角三角形,DG⊥EF,運用三線合一得出G為EF的中點,再根據直角三角形斜邊上的中線等于斜邊的一半,即可得出CG=GD;
②先根據等角的余角相等,得出DG=GH,再根據直角三角形的性質,得出EF=CH=13,最后運用勾股定理,在Rt△CEF中,求得EC的長度.
解答 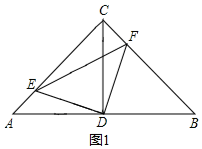 解:(1)如圖1,∵在△ABC中,AC=BC,∠ACB=90°,
解:(1)如圖1,∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠B=45°.
∵CD為邊AB上的中線,
∴CD⊥AB,AD=CD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCB,即∠A=∠DCF.
∵在△AED與△CFD中,
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCF}\\{AE=CF}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
∴∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)①如圖2,∵△DEF是等腰直角三角形,DG⊥EF,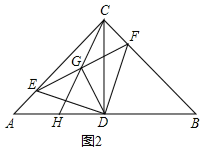
∴G為EF的中點,
∴Rt△DEF中,DG=$\frac{1}{2}$EF.
∵∠ECF=90°,G為EF的中點,
∴Rt△CEF中,GC=$\frac{1}{2}$EF.
∴CG=GD;
②由(1)可知,DG=CG,∠CDF=90°,
∴∠CDG=∠GCD,
又∵∠CDG+∠GDH=∠DCG+∠DHG=90°,
∴∠GDH=∠GHD,
∴DG=GH,
∴CG=GH=$\frac{1}{2}$CH,
∵∠ECF=90°,G為EF中點,
∴CG=$\frac{1}{2}$EF,
∴EF=CH=13,
由(1)可知,△AED≌△CFD,
∴AE=CF=5,
∴Rt△CEF中,EC=$\sqrt{E{F}^{2}-C{F}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12.
點評 本題屬于三角形綜合題,主要考查了等腰直角三角形的判定與性質,全等三角形的判定與性質,直角三角形斜邊上的中線性質以及勾股定理的綜合應用,解決問題的關鍵是掌握等腰三角形三線合一的性質,以及直角三角形中斜邊上的中線等于斜邊的一半.


科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:單選題
若x=3是方程x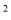 -3mx+6m=0的一個根,則m的值為( )
-3mx+6m=0的一個根,則m的值為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
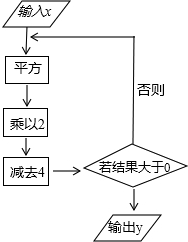 根據如圖所示的程序計算.
根據如圖所示的程序計算.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,正方形ABCD的四個頂點分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結論錯誤的是( )
如圖,正方形ABCD的四個頂點分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結論錯誤的是( )| A. | a=c | B. | 當a=b=c時,四邊形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面積為(a+b)2+c2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
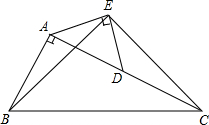 已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點,以AD為斜邊在△ABC外作等腰直角三角形AED,連結BE、EC.試猜想線段BE和EC有何關系,并證明你的猜想.
已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點,以AD為斜邊在△ABC外作等腰直角三角形AED,連結BE、EC.試猜想線段BE和EC有何關系,并證明你的猜想.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點M,若DM=1,求BC的值.
如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點M,若DM=1,求BC的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com