
 如圖,正六邊形ABCDEF內接于⊙O,過點O作OM⊥弦BC于點M,若⊙O的半徑為4,則OM和$\widehat{BC}$的長分別為( )
如圖,正六邊形ABCDEF內接于⊙O,過點O作OM⊥弦BC于點M,若⊙O的半徑為4,則OM和$\widehat{BC}$的長分別為( )| A. | 2,$\frac{π}{3}$ | B. | 2$\sqrt{3}$,π | C. | $\sqrt{3}$,$\frac{2π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
分析 如圖,連接OB、OC.首先證明△OBC是等邊三角形,求出BC、BM,根據勾股定理即可求出OM,利用弧長公式求出$\widehat{BC}$的長即可.
解答 解:如圖,連接OB、OC.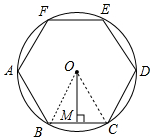
∵ABCDEF是正六邊形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等邊三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM=$\sqrt{O{B}^{2}-B{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
$\widehat{BC}$的長=$\frac{60π•4}{180}$=$\frac{4}{3}$π.
故選D.
點評 本題考查正多邊形與圓、等邊三角形的性質、勾股定理、弧長公式等知識,解題的關鍵是記住等邊三角形的性質,弧長公式,屬于基礎題,中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
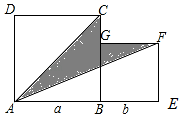 如圖,正方形ABCD和正方形BEFG平放在一起.
如圖,正方形ABCD和正方形BEFG平放在一起.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 160° | B. | 150° | C. | 120° | D. | 110° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
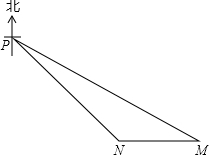 如圖,某海島上有一觀測點P,一天上午9:00觀測到一輪船在點M處,M在觀測點P南偏東60°方向上,漁船由東向西勻速航行跟蹤魚群,當天上午9:30漁船行至點N處,N在觀測點P的東南方向上,已知該漁船的速度為每小時40海里.
如圖,某海島上有一觀測點P,一天上午9:00觀測到一輪船在點M處,M在觀測點P南偏東60°方向上,漁船由東向西勻速航行跟蹤魚群,當天上午9:30漁船行至點N處,N在觀測點P的東南方向上,已知該漁船的速度為每小時40海里.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com