
 如圖,已知反比例函數y=$\frac{3}{x}$的圖象與正比例函數y=kx(k>0,k≠3),y=3x的圖象分別交于A,B,C,D四點.
如圖,已知反比例函數y=$\frac{3}{x}$的圖象與正比例函數y=kx(k>0,k≠3),y=3x的圖象分別交于A,B,C,D四點.分析 (1)先根據點A的坐標求出k的值,分別列方程組求四個交點的坐標;
(2)根據反比例函數是中心對稱圖形可知:OA=OB,OC=OD,所以對角線互相平分的四邊形是平行四邊形,則四邊形ACBD是平行四邊形;
(3)先列方程組求出點A的坐標,當四邊形ACBD是矩形時,OA=OC,根據第1問中點C的坐標利用勾股定理求出OC的長,由OA=OC列式可求得k的值,再求矩形的長和寬,代入面積公式可得矩形面積.
解答 解:(1)把A的坐標為(2,$\frac{3}{2}$)代入y=kx中得:2k=$\frac{3}{2}$,
k=$\frac{3}{4}$,
∴正比例函數解析式為:y=$\frac{3}{4}$x;
由題意得:$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=\frac{3}{4}x}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=\frac{3}{2}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-\frac{3}{2}}\end{array}\right.$,
$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=3x}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-3}\end{array}\right.$,
∴B(-2,-$\frac{3}{2}$),C(1,3),D(-1,-3);
(2)∵反比例函數y=$\frac{3}{x}$的圖象是關于原點O的中心對稱圖形
∴OA=OB,OC=OD
∴四邊形ACBD是平行四邊形;
(3)若四邊形ACBD是矩形,
∴AB=CD,
∵OA=OB,OC=OD,
∴OC=OA,
∵C(1,3),
∴OA=OC=$\sqrt{10}$,
由$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=kx}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=\sqrt{\frac{3}{k}}}\\{{y}_{1}=\sqrt{3k}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-\sqrt{\frac{3}{k}}}\\{{y}_{2}=-\sqrt{3k}}\end{array}\right.$,
∴A($\sqrt{\frac{3}{k}}$,$\sqrt{3k}$),
∴$(\sqrt{\frac{3}{k}})^{2}+(\sqrt{3k})^{2}$=($\sqrt{10}$)2,
3k2-10k+3=0,
(3k-1)(k-3)=0,
k1=$\frac{1}{3}$,k2=3(舍),
∴正比例函數解析式為:y=$\frac{1}{3}$x;
∴A(3,1),
分別過A、C作x軸、y軸的垂線,交于點E,則△AEC是直角三角形,
AE=3-1=2,CE=3-1=2,
由勾股定理得:AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(2\sqrt{10})^{2}-(2\sqrt{2})^{2}}$=4$\sqrt{2}$,
∴S矩形ABCD=BC•AC=4$\sqrt{2}$×$2\sqrt{2}$=16.
點評 本題是四邊形與函數的綜合題,考查了矩形、平行四邊形的性質和判定、一次函數和反比例函數的交點問題,確定兩函數交點時,將兩函數的解析式列方程組,其解就是交點坐標;同時要熟練掌握矩形、平行四邊形的性質和判定;注意數形結合的思想,及坐標與圖形的特點.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,直線y=-$\frac{3}{4}$x-3與x軸、y軸分別交于A、B兩點,C為x軸正半軸上一點,S△ABC=9.
如圖,在平面直角坐標系中,直線y=-$\frac{3}{4}$x-3與x軸、y軸分別交于A、B兩點,C為x軸正半軸上一點,S△ABC=9.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
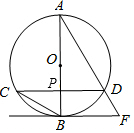 如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.
如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在矩形ABCD中,點P為AB上一個動點,以DP為折線翻折△APD得到△DPE,A的對應點為點E,連接BE,若AB=3,AD=4,當△BEP為直角三角形時,求AP的長.
如圖,在矩形ABCD中,點P為AB上一個動點,以DP為折線翻折△APD得到△DPE,A的對應點為點E,連接BE,若AB=3,AD=4,當△BEP為直角三角形時,求AP的長.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com