18. 某會(huì)議室用3盞燈照明，每盞燈各使用節(jié)能燈管一只，且型號(hào)相同。假定每盞燈能否正常照明只與燈管的壽命有關(guān)，該型號(hào)的燈管壽命為1年以上的概率為0.8，壽命為2年以上的概率為0.3，從使用之日起每滿1年進(jìn)行一次燈管更換工作，只更換已壞的燈管，平時(shí)不換。
（I）在第一次燈管更換工作中，求不需要更換燈管的概率；
（II）在第二次燈管更換工作中，對(duì)其中的某一盞燈來(lái)說(shuō)，求該燈需要更換燈管的概率；
（III）設(shè)在第二次燈管更換工作中，需要更換的燈管數(shù)為ξ，求ξ的分布列和期望。
17.如圖是函數(shù)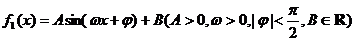
在同一個(gè)周期內(nèi)的圖像。（I）求函數(shù)
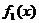的解析式；（II）將函數(shù)
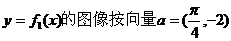平移，得到函數(shù)
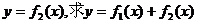的最大值，并求此時(shí)自變量x的集合。
16.在中學(xué)數(shù)學(xué)中，從特殊到一般，從具體到抽象是常見(jiàn)的一種思維方式。如從指數(shù)函數(shù)中可抽象出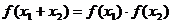
的性質(zhì)；從對(duì)數(shù)函數(shù)中可抽象出
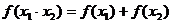的性質(zhì)，那么從函數(shù) （寫出一個(gè)具體函數(shù)即可）可抽象出
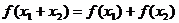的性質(zhì)。
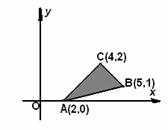
15.在如下圖所示的坐標(biāo)平面的可行域內(nèi)（包括邊界），目標(biāo)函數(shù) z＝x＋ay取得最小值的最優(yōu)解有無(wú)數(shù)個(gè)，則a= .
14.已知雙曲線的中心在原點(diǎn)O，焦點(diǎn)在x軸上，它的虛軸長(zhǎng)為2，且焦距是兩準(zhǔn)線間距離的2倍，則該雙曲線的方程為 。
13. 設(shè)
，則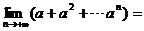
。
 |
