
2.(90年高考題)已知f(x)=x +ax+bx-8,且f(-2)=10,那么f(2)等于_____。
+ax+bx-8,且f(-2)=10,那么f(2)等于_____。
A. -26 B. -18 C. -10 D. 10
據題設條件作出所研究問題的曲線或有關圖形,借助幾何圖形的直觀性作出正確判斷的方法叫圖解法或數形結合法。
[例10](97年高考題)橢圖C與橢圓 +
+ =1關于直線x+y=0對稱,橢圓C的方程是_____。
=1關于直線x+y=0對稱,橢圓C的方程是_____。
A. +
+ =1 B.
=1 B.  +
+ =1
=1
C.  +
+ =1 D.
=1 D.  +
+ =1
=1
[解]圖解法:作出橢圓及對稱的橢圓C,由中心及焦點位置,容易得到選A。
[另解]直接法:設橢圓C上動點(x,y),則對稱點(-y,-x),代入已知橢圓方程得 +
+ =1,整理即得所求曲線C方程,所以選A。
=1,整理即得所求曲線C方程,所以選A。
[例11](87年高考題)在圓x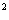 +y
+y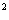 =4上與直線4x+3y-12=0距離最小的點的坐標是_____。
=4上與直線4x+3y-12=0距離最小的點的坐標是_____。
|
y
O
x |
A. ( ,
, ) B. (
) B. ( ,-
,- ) C. (-
) C. (- ,
, )
D. (-
)
D. (- ,-
,- )
)
 [解]圖解法:在同一直角坐標系中作出圓x
[解]圖解法:在同一直角坐標系中作出圓x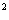 +y
+y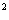 =4和直線4x+3y-12=0后,由圖可知距離最小的點在第一象限內,所以選A。
=4和直線4x+3y-12=0后,由圖可知距離最小的點在第一象限內,所以選A。
[直接法]先求得過原點的垂線,再與已知直線相交而得。
 M - i
2
M - i
2    |
[例12]已知復數z的模為2,則 |z-i| 的最大值為_______。
A. 1 B. 2 C.  D. 3
D. 3
[解]圖解法:由復數模的幾何意義,畫出右圖,可知當圓上的點到M的距離最大時即為|z-i|最大。所以選D;
[另解]不等式法或代數法或三角法:
|z-i|≤|z|+|i|=3,所以選D。
數形結合,借助幾何圖形的直觀性,迅速作正確的判斷是高考考查的重點之一;97年高考選擇題直接與圖形有關或可以用數形結合思想求解的題目約占50%左右。
從考試的角度來看,解選擇題只要選對就行,不管是什么方法,甚至可以猜測。但平時做題時要盡量弄清每一個選擇支正確理由與錯誤的原因,這樣,才會在高考時充分利用題目自身的提供的信息,化常規為特殊,避免小題作,真正做到熟練、準確、快速、順利完成三個層次的目標任務。
Ⅱ、鞏固性題組:
1.(86年高考題)函數y=( )
) +1的反函數是______。
+1的反函數是______。
A. y=log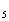 x+1 (x>0)
B. y=log
x+1 (x>0)
B. y=log 5+1 (x>0且x≠1)
5+1 (x>0且x≠1)
C. y=log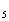 (x-1) (x>1) D. y=log
(x-1) (x>1) D. y=log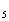 x-1 (x>1)
x-1 (x>1)
將各個選擇項逐一代入題設進行檢驗,從而獲得正確判斷的方法叫代入法,又稱為驗證法,即將各選擇支分別作為條件,去驗證命題,能使命題成立的選擇支就是應選的答案。
[例8](97年高考題)函數y=sin( -2x)+sin2x的最小正周期是_____。
-2x)+sin2x的最小正周期是_____。
A. B.
B.  C. 2
C. 2 D. 4
D. 4
[解]代入法:f(x+ )=sin[
)=sin[ -2(x+
-2(x+ )]+sin[2(x+
)]+sin[2(x+ )]=-f(x),而
)]=-f(x),而
f(x+π)=sin[ -2(x+π)]+sin[2(x+π)]=f(x)。所以應選B;
-2(x+π)]+sin[2(x+π)]=f(x)。所以應選B;
[另解]直接法:y= cos2x-
cos2x- sin2x+sin2x=sin(2x+
sin2x+sin2x=sin(2x+ ),T=π,選B。
),T=π,選B。
[例9](96年高考題)母線長為1的圓錐體積最大時,其側面展開圖的圓心角 等于_____。
等于_____。
A.  B.
B.
 C.
C.  D.
D.
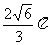
[解]代入法:四個選項依次代入求得r分別為: 、
、 、
、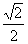 、
、 ,再求得h分別為:
,再求得h分別為: 、
、 、
、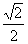 、
、 ,最后計算體積取最大者,選D。
,最后計算體積取最大者,選D。
[另解]直接法:設底面半徑r,則V= πr
πr
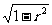 =
=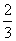 π
π

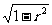 ≤…
≤…
其中 =
=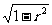 ,得到r=
,得到r= ,所以
,所以 =2π
=2π /1=
/1=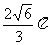 ,選D。
,選D。
代入法適應于題設復雜,結論簡單的選擇題。若能據題意確定代入順序,則能較大提高解題速度。
從題設條件出發,運用定理、性質、公式推演,根據“四選一”的指令,逐步剔除干擾項,從而得出正確判斷的方法叫篩選法或剔除法。
[例6](95年高考題)已知y=log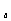 (2-ax)在[0,1]上是x的減函數,則a的取值范圍是_____。
(2-ax)在[0,1]上是x的減函數,則a的取值范圍是_____。
A. [0,1] B. (1,2] C. (0,2) D. [2,+∞)
[解]∵ 2-ax是在[0,1]上是減函數,所以a>1,排除答案A、C;若a=2,由2-ax>0得x<1,這與[0,1]不符合,排除答案C。所以選B。
[例7](88年高考題)過拋物線y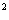 =4x的焦點,作直線與此拋物線相交于兩點P和Q,那么線段PQ中點的軌跡方程是______。
=4x的焦點,作直線與此拋物線相交于兩點P和Q,那么線段PQ中點的軌跡方程是______。
A. y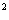 =2x-1 B. y
=2x-1 B. y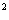 =2x-2 C. y
=2x-2 C. y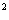 =-2x+1 D. y
=-2x+1 D. y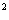 =-2x+2
=-2x+2
[解]篩選法:由已知可知軌跡曲線的頂點為(1,0),開口向右,由此排除答案A、C、D,所以選B;
[另解]直接法:設過焦點的直線y=k(x-1),則 ,消y得:
,消y得:
k x
x -2(k
-2(k +2)x+k
+2)x+k =0,中點坐標有
=0,中點坐標有 ,消k得y
,消k得y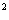 =2x-2,選B。
=2x-2,選B。
篩選法適應于定性型或不易直接求解的選擇題。當題目中的條件多于一個時,先根據某些條件在選擇支中找出明顯與之矛盾的,予以否定,再根據另一些條件在縮小的選擇支的范圍那找出矛盾,這樣逐步篩選,直到得出正確的選擇。它與特例法、圖解法等結合使用是解選擇題的常用方法,近幾年高考選擇題中約占40%。
用特殊值(特殊圖形、特殊位置)代替題設普遍條件,得出特殊結論,對各個選項進行檢驗,從而作出正確判斷的方法叫特例法。常用的特例有特殊數值、特殊數列、特殊函數、特殊圖形、特殊角、特殊位置等。
[例4](97年高考題)定義在區間(-∞,∞)的奇函數f(x)為增函數,偶函數g(x)在區間[0,+∞)的圖象與f(x)的圖象重合,設a>b>0,給出下列不等式①f(b)-f(-a)>g(a)-g(-b);②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a);④f(a)-f(-b)<g(b)-g(-a).其中成立的是( )
A. ①與④ B. ②與③ C. ①與③ D. ②與④
[解]令f(x)=x,g(x)=|x|,a=2,b=1,則:f(b)-f(-a)=1-(-2)=3, g(a)-g(-b)=2-1=1,得到①式正確;f(a)-f(-b)=2-(-1)=3, g(b)-g(-a)=1-2=-1,得到③式正確。所以選C。
[另解]直接法:f(b)-f(-a)=f(b)+f(a),g(a)-g(-b)=g(a)-g(b)=f(a)-f(b),從而①式正確;f(a)-f(-b)=f(a)+f(b),g(b)-g(-a)=g(b)-g(a)=f(b)-f(a),從而③式正確。所以選C。
[例5](85年高考題)如果n是正偶數,則C +C
+C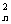 +…+C
+…+C +C
+C =______。
=______。
A. 2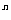 B. 2
B. 2 C. 2
C. 2 D. (n-1)2
D. (n-1)2
[解]用特值法:當n=2時,代入得C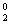 +C
+C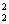 =2,排除答案A、C;當n=4時,代入得C
=2,排除答案A、C;當n=4時,代入得C +C
+C +C
+C =8,排除答案D。所以選B。
=8,排除答案D。所以選B。
[另解]直接法:由二項展開式系數的性質有C +C
+C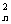 +…+C
+…+C +C
+C =2
=2 ,選B。
,選B。
當正確的選擇對象,在題設普遍條件下都成立的情況下,用特殊值(取得愈簡單愈好)進行探求,從而清晰、快捷地得到正確的答案,即通過對特殊情況的研究來判斷一般規律,是解答本類選擇題的最佳策略。近幾年高考選擇題中可用或結合特例法解答的約占30%左右。
直接從題設條件出發,運用有關概念、性質、定理、法則等知識,通過推理運算,得出結論,再對照選擇項,從中選正確答案的方法叫直接法。
[例1](96年高考題)若sin x>cos
x>cos x,則x的取值范圍是______。
x,則x的取值范圍是______。
A.{x|2k -
-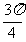 <x<2k
<x<2k +
+ ,k
,k Z} B.
{x|2k
Z} B.
{x|2k +
+ <x<2k
<x<2k +
+ ,k
,k Z}
Z}
C. {x|k -
- <x<k
<x<k +
+ ,k
,k Z} D. {x|k
Z} D. {x|k +
+ <x<k
<x<k +
+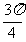 ,k
,k Z}
Z}
[解]直接解三角不等式:由sin x>cos
x>cos x得cos
x得cos x-sin
x-sin x<0,即cos2x<0,所以:
x<0,即cos2x<0,所以:
 +2kπ<2x<
+2kπ<2x< +2kπ,選D;
+2kπ,選D;
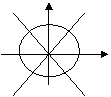
[另解]數形結合法:由已知得|sinx|>|cosx|,畫出單位圓:
利用三角函數線,可知選D。
[例2](96年高考題)設f(x)是(-∞,∞)是的奇函數,f(x+2)=-f(x),當0≤x≤1時,f(x)=x,則f(7.5)等于______。
A. 0.5 B. -0.5 C. 1.5 D. -1.5
[解]由f(x+2)=-f(x)得f(7.5)=-f(5.5)=f(3.5)=-f(1.5)=f(-0.5),由f(x)是奇函數得f(-0.5)=-f(0.5)=-0.5,所以選B。
也可由f(x+2)=-f(x),得到周期T=4,所以f(7.5)=f(-0.5)=-f(0.5)=-0.5。
[例3](87年高考題)七人并排站成一行,如果甲、乙兩人必需不相鄰,那么不同的排法的種數是_____。
A. 1440 B. 3600 C. 4320 D. 4800
[解一]用排除法:七人并排站成一行,總的排法有P 種,其中甲、乙兩人相鄰的排法有2×P
種,其中甲、乙兩人相鄰的排法有2×P 種。因此,甲、乙兩人必需不相鄰的排法種數有:P
種。因此,甲、乙兩人必需不相鄰的排法種數有:P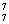 -2×P
-2×P =3600,對照后應選B;
=3600,對照后應選B;
[解二]用插空法:P ×P
×P =3600。
=3600。
直接法是解答選擇題最常用的基本方法,低檔選擇題可用此法迅速求解。直接法適用的范圍很廣,只要運算正確必能得出正確的答案。提高直接法解選擇題的能力,準確地把握中檔題目的“個性”,用簡便方法巧解選擇題,是建在扎實掌握“三基”的基礎上,否則一味求快則會快中出錯。
一些計算過程復雜的代數、三角、解析幾何問題,可以作出有關函數的圖像或者構造適當的幾何圖形,利用圖示輔助進行直觀分析,從而得出結論。這也就是數形結合的解題方法。
    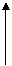  y y
 O 2 x
O 2 x |
[例5]不等式 >x+1的解集是
。
>x+1的解集是
。
[解]如圖,在同一坐標系中畫出函數y= 與y=x+1的圖像,由圖中可以直觀地得到:-
與y=x+1的圖像,由圖中可以直觀地得到:- ≤x<2,所以所求解集是[-
≤x<2,所以所求解集是[- ,2)。
,2)。
     y
O 1 3|k| x y
O 1 3|k| x |
[例6](93年高考題)若雙曲線 -
- =1與圓x
=1與圓x +y
+y =1沒有公共點,則實數k的取值范圍是
。
=1沒有公共點,則實數k的取值范圍是
。
[解]在同一坐標系中作出雙曲線 -
- =1與圓x
=1與圓x +y
+y =1,由雙曲線的頂點位置的坐標,可以得到|3k|>1,故求得實數k的取值范圍是k>
=1,由雙曲線的頂點位置的坐標,可以得到|3k|>1,故求得實數k的取值范圍是k> 或k<-
或k<- 。
。
當填空題已知條件中含有某些不確定的量,但題目暗示答案可能是一個定值時,可以將變量取一些特殊數值、特殊位置、或者一種特殊情況來求出這個定值,這樣,簡化了推理、論證的過程。
[例3](89年高考題)已知(1-2x) =a
=a +a
+a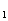 x+a
x+a x
x +…+a
+…+a x
x ,那么a
,那么a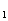 +a
+a +…+a
+…+a = 。
= 。
[解]令x=1,則有(-1) =a
=a +a
+a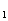 +a
+a +…+a
+…+a =-1;令x=0,則有a
=-1;令x=0,則有a =1。所以a
=1。所以a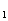 +a
+a +…+a
+…+a =-1-1=-2。
=-1-1=-2。
[例4](90年高考題)在三棱柱ABC-A’B’C’中,若E、F分別為AB、AC的中點,平面EB’C’F將三棱柱分成體積為V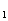 、V
、V 的兩部分,那么V
的兩部分,那么V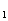 :V
:V = 。
= 。
[解]由題意分析,結論與三棱柱的具體形狀無關,因此,可取一個特殊的直三棱柱,其底面積為4,高為1,則體積V=4,而V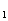 =
= (1+
(1+ +4)=
+4)= ,V
,V =V-V
=V-V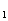 =
= ,則V
,則V :V
:V =7:5。
=7:5。
直接法就是根據數學概念,或者運用數學的定義、定理、法則、公式等,從已知條件出發,進行推理或者計算得出結果后,將所得結論填入空位處,它是解填空題最基本、最常用的方法。
[例1](94年高考題)已知sinθ+cosθ= ,θ∈(0,π),則ctgθ的值是 。
,θ∈(0,π),則ctgθ的值是 。
[解]已知等式兩邊平方得sinθcosθ=- ,解方程組得sinθ=
,解方程組得sinθ= ,cosθ=
,cosθ= ,故答案為:-
,故答案為:- 。
。
[另解]設tg =t,再利用萬能公式求解。
=t,再利用萬能公式求解。
[例2](95年高考題)方程log (x+1)
(x+1) +log
+log (x+1)=5的解是 。
(x+1)=5的解是 。
[解]由換底公式得4log (x+1)+log
(x+1)+log (x+1)=5,即log
(x+1)=5,即log (x+1)=1,解得x=3。
(x+1)=1,解得x=3。
14. 若方程lg(kx)=2lg(x+1)只有一個實數解,求常數k的取值范圍。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com