
3. 方程2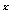 =x
=x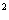 +2x+1的實數解的個數是_____。
+2x+1的實數解的個數是_____。
A. 1 B. 2 C. 3 D.以上都不對
2. 已知集合P={(x,y)|y=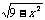 }、Q={(x,y)|y=x+b},若P∩Q≠φ,則b的取值范圍是____。
}、Q={(x,y)|y=x+b},若P∩Q≠φ,則b的取值范圍是____。
A. |b|<3 B. |b|≤3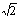 C. -3≤b≤3
C. -3≤b≤3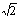 D. -3<b<3
D. -3<b<3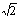
1. 已知5x+12y=60,則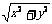 的最小值是_____。
的最小值是_____。
A. 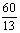 B.
B. 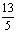 C.
C. 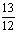 D. 1
D. 1
10. 滿足方程|z+3-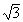 i|=
i|=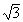 的輻角主值最小的復數z是_____。
的輻角主值最小的復數z是_____。
[簡解]1小題:將不等式解集用數軸表示,可以看出,甲=>乙,選A;
2小題:由已知畫出對數曲線,選B;
3小題:設sinx=t后借助二次函數的圖像求f(x)的最小值,選D;
4小題:由奇函數圖像關于原點對稱畫出圖像,選B;
5小題:將幾個集合的幾何意義用圖形表示出來,選B;
6小題:利用單位圓確定符號及象限;選B;
7小題:利用單位圓,選A;
8小題:將復數表示在復平面上,選B;
9小題:轉化為圓上動點與原點連線的斜率范圍問題;選D;
10小題:利用復平面上復數表示和兩點之間的距離公式求解,答案-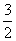 +
+ i。
i。
[注] 以上各題是歷年的高考客觀題,都可以借助幾何直觀性來處理與數有關的問題,即借助數軸(①題)、圖像(②、③、④、⑤題)、單位圓(⑥、⑦題)、復平面(⑧、⑩題)、方程曲線(⑨題)。
    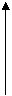  y
4 y=1-m
1
O 2 3 x y
4 y=1-m
1
O 2 3 x |
Ⅱ、示范性題組:
例1. 若方程lg(-x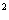 +3x-m)=lg(3-x)在x∈(0,3)內有唯一解,求實數m的取值范圍。
+3x-m)=lg(3-x)在x∈(0,3)內有唯一解,求實數m的取值范圍。
[分析]將對數方程進行等價變形,轉化為一元二次方程在某個范圍內有實解的問題,再利用二次函數的圖像進行解決。
[解] 原方程變形為 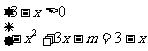
即: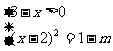
設曲線y =(x-2)
=(x-2)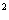 , x∈(0,3)和直線y
, x∈(0,3)和直線y =1-m,圖像如圖所示。由圖可知:
=1-m,圖像如圖所示。由圖可知:
① 當1-m=0時,有唯一解,m=1;
②當1≤1-m<4時,有唯一解,即-3<m≤0,
∴ m=1或-3<m≤0
此題也可設曲線y =-(x-2)
=-(x-2)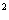 +1 , x∈(0,3)和直線y
+1 , x∈(0,3)和直線y =m后畫出圖像求解。
=m后畫出圖像求解。
[注] 一般地,方程的解、不等式的解集、函數的性質等進行討論時,可以借助于函數的圖像直觀解決,簡單明了。此題也可用代數方法來討論方程的解的情況,還可用分離參數法來求(也注意結合圖像分析只一個x值)。
     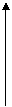  y A
D
O B x y A
D
O B x
C |
例2. 設|z |=5,|z
|=5,|z |=2, |z
|=2, |z -
-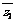 |=
|=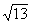 ,求
,求 的值。
的值。
[分析] 利用復數模、四則運算的幾何意義,將復數問題用幾何圖形幫助求解。
[解] 如圖,設z =
=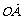 、z
、z =
=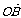 后,則
后,則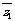 =
=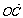 、
、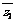 =
=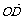 如圖所示。
如圖所示。
由圖可知,| |=
|=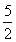 ,∠AOD=∠BOC,由余弦定理得:
,∠AOD=∠BOC,由余弦定理得:
cos∠AOD=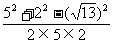 =
=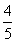
∴  =
=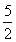 (
(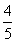 ±
± i)=2±
i)=2±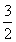 i
i
   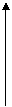  y A
D
O x y A
D
O x
|
[另解]設z =
=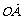 、
、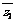 =
=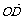 如圖所示。則|
如圖所示。則|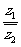 |=
|=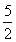 ,且
,且
cos∠AOD=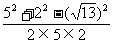 =
=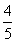 ,sin∠AOD=±
,sin∠AOD=±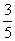 ,
,
所以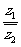 =
=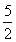 (
(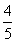 ±
± i)=2±
i)=2±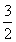 i,即
i,即 =2±
=2±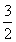 i。
i。
[注]本題運用“數形結合法”,把共軛復數的性質與復平面上的向量表示、代數運算的幾何意義等都表達得淋漓盡致,體現了數形結合的生動活潑。 一般地,復數問題可以利用復數的幾何意義而將問題變成幾何問題,也可利用復數的代數形式、三角形式、復數性質求解。
本題設三角形式后轉化為三角問題的求解過程是:設z =5(cosθ
=5(cosθ +isinθ
+isinθ ),z
),z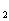 =+isinθ
=+isinθ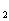 ),則|z
),則|z -
-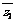 |=|(5cosθ
|=|(5cosθ -2cosθ
-2cosθ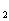 )+(5sinθ
)+(5sinθ +2sinθ
+2sinθ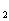 )i|=
)i|=
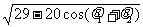 =
= ,所以cos(θ
,所以cos(θ +θ
+θ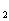 )=
)=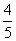 ,sin(θ
,sin(θ +θ
+θ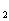 )=±
)=±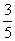 ,
,
 =
=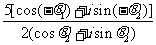 =
=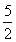 [cos(θ
[cos(θ +θ
+θ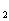 )+isin(θ
)+isin(θ +θ
+θ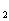 )]=
)]=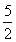 (
(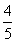 ±
± i)=2±
i)=2±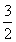 i。
i。
本題還可以直接利用復數性質求解,其過程是:由|z -
-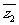 |=
|=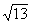 得:
得:
(z -
-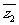 )(
)(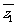 -z
-z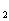 )=z
)=z
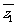 +z
+z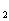
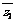 -z
-z z
z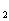 -
-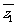
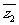 =25+4-z
=25+4-z z
z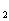 -
-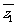
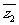 =13,
=13,
所以z z
z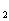 +
+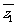
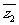 =16,再同除以z
=16,再同除以z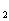
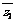 得
得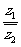 +
+ =4,設
=4,設 =z,解得z=2±
=z,解得z=2±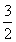 i。
i。
幾種解法,各有特點,由于各人的立足點與思維方式不同,所以選擇的方法也有別。一般地,復數問題可以應用于求解的幾種方法是:直接運用復數的性質求解;設復數的三角形式轉化為三角問題求解;設復數的代數形式轉化為代數問題求解;利用復數的幾何意義轉化為幾何問題求解。
例3. 直線L的方程為:x=-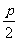 (p>0),橢圓中心D(2+
(p>0),橢圓中心D(2+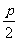 ,0),焦點在x軸上,長半軸為2,短半軸為1,它的左頂點為A。問p在什么范圍內取值,橢圓上有四個不同的點,它們中每一個點到點A的距離等于該點到直線L的距離?
,0),焦點在x軸上,長半軸為2,短半軸為1,它的左頂點為A。問p在什么范圍內取值,橢圓上有四個不同的點,它們中每一個點到點A的距離等于該點到直線L的距離?
[分析] 由拋物線定義,可將問題轉化成:p為何值時,以A為焦點、L為準線的拋物線與橢圓有四個交點,再聯立方程組轉化成代數問題(研究方程組解的情況)。
[解] 由已知得:a=2,b=1, A(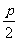 ,0),設橢圓與雙曲線方程并聯立有:
,0),設橢圓與雙曲線方程并聯立有:
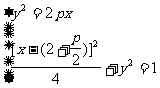 ,消y得:x
,消y得:x -(4-7p)x+(2p+
-(4-7p)x+(2p+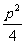 )=0
)=0
所以△=16-64p+48p >0,即6p
>0,即6p -8p+2>0,解得:p<
-8p+2>0,解得:p<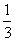 或p>1。
或p>1。
結合范圍(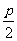 ,4+
,4+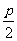 )內兩根,設f(x)=x
)內兩根,設f(x)=x -(4-7p)x+(2p+
-(4-7p)x+(2p+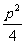 ),
),
所以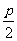 <
<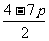 <4+
<4+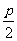 即p<
即p< ,且f(
,且f(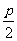 )>0、f(4+
)>0、f(4+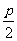 )>0即p>-4+3
)>0即p>-4+3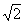 。
。
結合以上,所以-4+3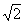 <p<
<p<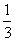 。
。
[注] 本題利用方程的曲線將曲線有交點的幾何問題轉化為方程有實解的代數問題。一般地,當給出方程的解的情況求參數的范圍時可以考慮應用了“判別式法”,其中特別要注意解的范圍。另外,“定義法”、“數形結合法”、“轉化思想”、“方程思想”等知識都在本題進行了綜合運用。
例4. 設a、b是兩個實數,A={(x,y)|x=n,y=na+b} (n∈Z),B={(x,y)|x=m,y=3m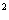 +15} (m∈Z),C={(x,y)|x
+15} (m∈Z),C={(x,y)|x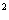 +y
+y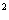 ≤144},討論是否,使得A∩B≠φ與(a,b)∈C同時成立。(85年高考)
≤144},討論是否,使得A∩B≠φ與(a,b)∈C同時成立。(85年高考)
[分析]集合A、B都是不連續的點集,“存在a、b,使得A∩B≠φ”的含意就是“存在a、b使得na+b=3n +15(n∈Z)有解(A∩B時x=n=m)。再抓住主參數a、b,則此問題的幾何意義是:動點(a,b)在直線L:nx+y=3n
+15(n∈Z)有解(A∩B時x=n=m)。再抓住主參數a、b,則此問題的幾何意義是:動點(a,b)在直線L:nx+y=3n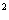 +15上,且直線與圓x
+15上,且直線與圓x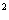 +y
+y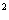 =144有公共點,但原點到直線L的距離≥12。
=144有公共點,但原點到直線L的距離≥12。
[解] 由A∩B≠φ得:na+b=3n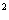 +15 ;
+15 ;
設動點(a,b)在直線L:nx+y=3n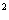 +15上,且直線與圓x
+15上,且直線與圓x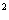 +y
+y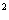 =144有公共點,
=144有公共點,
所以圓心到直線距離d=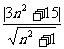 =3(
=3(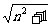 +
+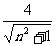 )≥12
)≥12
∵ n為整數 ∴ 上式不能取等號,故a、b不存在。
[注] 集合轉化為點集(即曲線),而用幾何方法進行研究。此題也屬探索性問題用數形結合法解,其中還體現了主元思想、方程思想,并體現了對有公共點問題的恰當處理方法。
本題直接運用代數方法進行解答的思路是:
由A∩B≠φ得:na+b=3n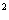 +15 ,即b=3n
+15 ,即b=3n +15-an (①式);
+15-an (①式);
由(a,b)∈C得,a +b
+b ≤144 (②式);
≤144 (②式);
把①式代入②式,得關于a的不等式:
(1+n )a
)a -2n(3n
-2n(3n +15)a+(3n
+15)a+(3n +15)
+15) -144≤0 (③式),
-144≤0 (③式),
它的判別式△=4n (3n
(3n +15)
+15) -4(1+n
-4(1+n )[(3n
)[(3n +15)
+15) -144]=-36(n
-144]=-36(n -3)
-3)
因為n是整數,所以n -3≠0,因而△<0,又因為1+n
-3≠0,因而△<0,又因為1+n >0,故③式不可能有實數解。
>0,故③式不可能有實數解。
所以不存在a、b,使得A∩B≠φ與(a,b)∈C同時成立
Ⅲ、鞏固性題組:
9. 如果實數x、y滿足等式(x-2)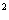 +y
+y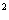 =3,那么
=3,那么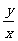 的最大值是_____。 (90年全國理)
的最大值是_____。 (90年全國理)
A.  B.
B. 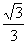 C.
C. 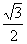 D.
D.
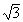
8. 若復數z的輻角為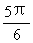 ,實部為-2
,實部為-2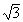 ,則z=_____。
,則z=_____。
A. -2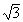 -2i B. -2
-2i B. -2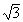 +2i C. -2
+2i C. -2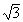 +2
+2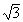 i D. -2
i D. -2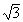 -2
-2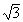 i
i
7. 已知集合E={θ|cosθ<sinθ,0≤θ≤2π},F={θ|tgθ<sinθ},那么E∩F的區間是_____。(93年全國文理)
A. (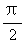 ,π) B. (
,π) B. (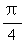 ,
,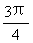 ) C. (π,
) C. (π, 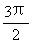 ) D. (
) D. (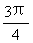 ,
,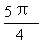 )
)
6. 如果θ是第二象限的角,且滿足cos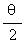 -sin
-sin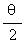 =
= ,那么
,那么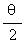 是_____。
是_____。
A.第一象限角 B.第三象限角 C.可能第一象限角,也可能第三象限角 D.第二象限角
5. 設全集I={(x,y)|x,y∈R},集合M={(x,y)|  =1},N={(x,y)|y≠x+1},那么
=1},N={(x,y)|y≠x+1},那么 等于_____。 (90年全國)
等于_____。 (90年全國)
A. φ B. {(2,3)} C. (2,3) D. {(x,y)|y=x+1
4. 如果奇函數f(x)在區間[3,7]上是增函數且最小值是5,那么f(x)的[-7,-3]上是____。(91年全國)
A.增函數且最小值為-5 B.增函數且最大值為-5
C.減函數且最小值為-5 D.減函數且最大值為-5
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com