
4.(2005全國Ⅲ)已知向量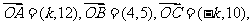 ,且A.B.C三點共線,則k= .
,且A.B.C三點共線,則k= .
3.已知向量a、b滿足|a|=1,|b|=2,|a-b|=2,則|a+b|等于 ( )
A.1 B.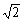 C.
C.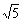 D.
D.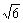
剖析:欲求|a+b|,一是設出a、b的坐標求,二是直接根據向量模計算.
2.平面上A(-2,1),B(1,4),D(4,-3),C點滿足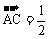
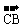 ,連DC并延長至E,使|
,連DC并延長至E,使|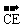 |=
|=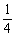 |
|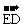 |,則點E坐標為:
( )
|,則點E坐標為:
( )
A、(-8,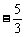 ) B、(
) B、(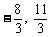 ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,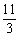 )
)
1.(2006山東)設向量a=(1,-3),b=(-2,4),c=(-1,-2),若表示向量4a、4b-2c、2(a-c)、d的有向線段依次首尾相接能構成四邊形,則向量d為 ( )
A.(2,6) B.(-2,6) C.(2,-6) D.(-2,-6)
3. 設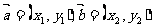 則
則
向量共線: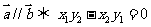
向量垂直: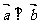 ,
,
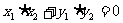
2.平面向量的坐標運算
(1)
若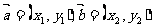 ,則
,則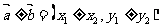
(2)
若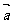 =(x,y),則
=(x,y),則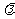
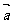 =(
=(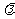 x,
x, 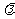 y)
y)
(3)
若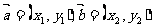 ,則
,則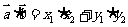
1.平面向量的坐標表示:在直角坐標系中,分別取與x軸、y軸方向相同的兩個單位向量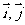 作為基底。由平面向量的基本定理知,該平面內的任一向量
作為基底。由平面向量的基本定理知,該平面內的任一向量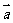 可表示成
可表示成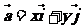 ,由于
,由于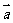 與數對(x,y)是一一對應的,因此把(x,y)叫做向量
與數對(x,y)是一一對應的,因此把(x,y)叫做向量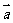 的坐標,記作
的坐標,記作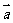 =(x,y),其中x叫作
=(x,y),其中x叫作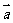 在x軸上的坐標,y叫做在y軸上的坐標。
在x軸上的坐標,y叫做在y軸上的坐標。
(1) 若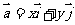 ,則
,則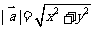
(2)若A(x1,y1),B(x2,y2)則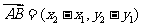 ,
,
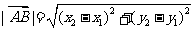
表示相等向量的有向線段的始點、終點的坐標未必相同.
(3) 向量相等ó坐標相同。
2.掌握平面向量的坐標運算,掌握共線向量的坐標表示;
1.理解平面向量的坐標概念;
26. 導數復習要注意哪些問題?
①導數的幾何意義即曲線在該點處的切線的斜率,學會定義的多種變形。
②利用導數可以證明或判斷函數的單調性,注意當≥0或f ’(x)≤0,帶上等號。
利用導數可以證明或判斷函數的單調性,注意當≥0或f ’(x)≤0,帶上等號。
③f ’(x0)=0是函數f(x)在x0處取得極值的非充分非必要條件,f(x)在x0處取得極值的充分要條件是什么?
④利用導數求最值的步驟:先找定義域 再求出導數為0及導數不存在的的點,然后比較定義域的端點導數為0的點對應函數值的大小,其中最大的就是最大值,最小就為最小值。
⑤求函數極值的方法:先找定義域,再求導,找出定義域的分界點,列表求出極值。告別特別是給出函數的極大值條件,一定要驗證是否在該處取得極大值 ,否則條件沒有用完,這一點一定要切記。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com