1．
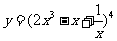；2．
；
4．
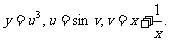
說明：分不清復合函數的復合關系，忽視最外層和中間變量都是基本函數的結構形式，而最內層可以是關于自變量x的基本函數，也可以是關于自變量的基本函數經過有限次的四則運算而得到的函數，導致陷入解題誤區，達不到預期的效果．
求函數的導數
例 求下列函數的導數．
3．
；
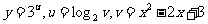2．
；
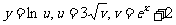1．
；
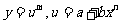3．
；4．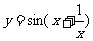
。
分析：由復合函數的定義可知，中間變量的選擇應是基本函數的結構，解決這類問題的關鍵是正確分析函數的復合層次，一般是從最外層開始，由外及里，一層一層地分析，把復合函數分解成若干個常見的基本函數，逐步確定復合過程．
解：函數的復合關系分別是
1．
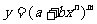；2．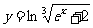
；
4．兩端取對數，得
，
兩邊對x求導，得
∴
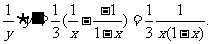
說明：對數求導法則實質上是復合函數求導法則的應用．從多角度分析和探索解決問題的途徑，能運用恰當合理的思維視力，把問題的隱含挖掘出來加以利用，會使問題的解答避繁就簡，化難為易，收到出奇制勝的效果．解決這類問題常見的錯誤是不注意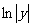
是關于x的復合函數．
指對數函數的概念揭示了各自存在的條件、基本性質及其幾何特征，恰當地引入對數求導的方法，從不同的側面分析轉化，往往可避免繁瑣的推理與運算，使問題得以解決．
3．兩端取對數，得
，
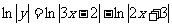兩端對x求導，得
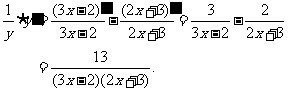
2．注意到
，兩端取對數，得
∴
∴
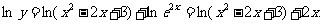
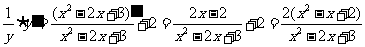
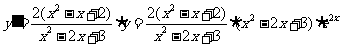
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com