
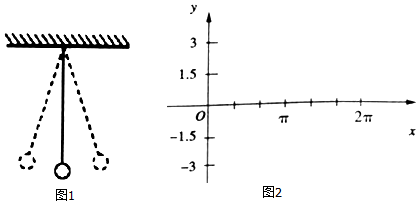
分析 (1)利用函數解析式求解即可.
(2)求出函數的周期,然后求解即可.
(3)畫出函數的圖象,利用已知條件通過概率轉化求解即可.
解答 解:(1)小球擺動時,離開平衡位置的位移s(單位:cm)與時間t(單位:s)的函數關系是:
s=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$),t∈[0,+∞),當t=0時,s=3cos$\frac{π}{3}$=$\frac{3}{2}$,
即小球離開平衡位置的位移s是$\frac{3}{2}cm$;
(2)周期$T=\frac{2π}{\sqrt{\frac{g}{l}}}$=2$π\sqrt{\frac{l}{g}}$=$2π\sqrt{\frac{40}{1000}}$=$\frac{2π}{5}$,所以頻率$f=\frac{1}{T}=\frac{5}{2π}$,即小球每1s能往復擺動$\frac{5}{2π}$次.
要使小球擺動的周期是1s,即$T=2π\sqrt{\frac{l}{g}}=2π\sqrt{\frac{l}{1000}}=1$,
解得$l=\frac{250}{π^2}$,即線的長度應該調整為$\frac{250}{π^2}cm$.
(3)$f(x)=3cos(x+\frac{π}{3}),x∈[0,2π)$的圖象,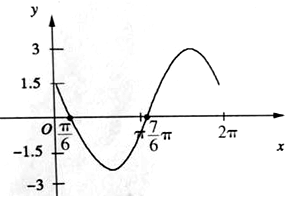
由題意可知,設事件A=“小球離開平衡位置的距離(位移的絕對值)比t=0時小球離開平衡位置的距離小”,只需$|3cos(x+\frac{π}{3})|≤\frac{3}{2}$,解得$0≤x≤\frac{π}{3}$或$π≤x≤\frac{4π}{3}$,由幾何概型可知,$P(A)=\frac{{(\frac{π}{3}-0)+(\frac{4π}{3}-π)}}{2π}=\frac{1}{3}$,所以估計符合條件的大約有$300×\frac{1}{3}=100$張.
點評 本題考查三角函數的化簡求值,三角函數的圖象的應用,概率的求法,考查計算能力.


科目:高中數學 來源: 題型:解答題
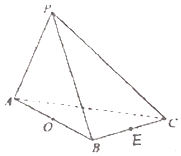 在三棱錐P-ABC中,△PAC和△PBC是邊長為$\sqrt{2}$的等邊三角形,AB=2,O是AB中點,E是BC中點.
在三棱錐P-ABC中,△PAC和△PBC是邊長為$\sqrt{2}$的等邊三角形,AB=2,O是AB中點,E是BC中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com