
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
分析 利用已知條件求出A,通過正弦定理求出B,然后求解C,利用三角形的面積公式求解即可.
解答 解:在△ABC中,角A,B,C的對邊分別為a,b,c,若a=2,b=sinA+cosA=$\sqrt{2}$,
可得$\sqrt{2}$sin(A+$\frac{π}{4}$)=$\sqrt{2}$,可得A=$\frac{π}{4}$,
由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{2}$=$\frac{1}{2}$,
∵a>b,∴A>B,可得B=$\frac{π}{6}$,所以C=$\frac{7π}{12}$,
則△ABC的面積為:$\frac{1}{2}absinC$=$\frac{1}{2}×2×\sqrt{2}×sin\frac{7π}{12}$=$\frac{\sqrt{2}(\sqrt{6}+\sqrt{2})}{4}$=$\frac{\sqrt{3}+1}{2}$.
故選:D.
點評 本題考查正弦定理的應用,三角形的面積公式的應用,注意正弦定理以及三角形邊角關系的應用,是易錯點.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
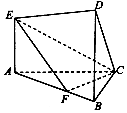 在如圖所示的幾何體中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如圖所示的幾何體中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | S>$\frac{1}{2}$ | B. | S>$\frac{3}{5}$ | C. | S>$\frac{7}{10}$ | D. | S>$\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com