
江蘇省2009屆高考數學精編模擬試題(二)
一.填空題
1 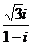 的共軛復數是
的共軛復數是
3.在三棱錐的六條棱中任意選擇兩條,則這兩條棱是一對異面直線的概率
4.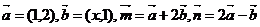 ,且
,且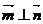 ,則
,則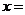
5.函數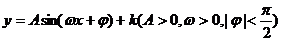 的圖象如下,則y的表達式是
的圖象如下,則y的表達式是
6.設二次函數 的導數為
的導數為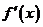 ,
,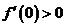 ,對于任意的實數
,對于任意的實數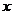 恒有
恒有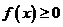 ,則
,則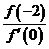 的最小值是
的最小值是
7.在等差數列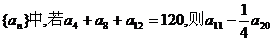 的值是
的值是
8.若直線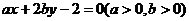 始終平分圓的周
始終平分圓的周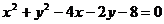 長,則
長,則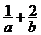 的最小值為
的最小值為
9 .一個總體共有100個個體,隨機編號0,1,2,…,99,按從小到大的編號順序平均分成10個小組,組號依次為1,2,3,…,10,現用系統抽樣方法抽取一個容量為10的樣本,規定如果在第1組隨機抽取的號碼為m,那么在第k組中抽取的號碼個位數字與m+k的個位數字相同,若m=4,則在第6組中抽取的號碼是
.一個總體共有100個個體,隨機編號0,1,2,…,99,按從小到大的編號順序平均分成10個小組,組號依次為1,2,3,…,10,現用系統抽樣方法抽取一個容量為10的樣本,規定如果在第1組隨機抽取的號碼為m,那么在第k組中抽取的號碼個位數字與m+k的個位數字相同,若m=4,則在第6組中抽取的號碼是
10. 、設球的半徑為R, P、Q是球面上北緯600圈上的兩點,這兩點在緯度圈上的劣弧的長是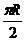 ,則這兩點的球面距離是
,則這兩點的球面距離是
11. 過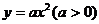 的焦點
的焦點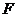 作直線交拋物線與
作直線交拋物線與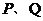 兩點,若
兩點,若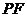 與
與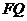 的長分別是
的長分別是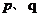 ,則
,則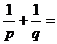
12. 一個幾何的三視圖如圖所示:其中,正視圖中△ABC的邊長是2的正三角形,俯視圖為正六邊形,那么該幾何體幾的體積為 .
13. 已知0<t<1,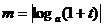 、
、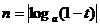 ,則
,則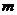 與
與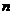 的大小關系為______.
的大小關系為______.
14、不論k為何實數,直線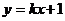 與曲線
與曲線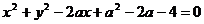 恒有交點,則實數a的取值范圍是 。
恒有交點,則實數a的取值范圍是 。
二.解答題
15. 已知:復數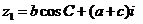 ,
,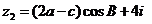 ,且
,且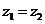 ,其中
,其中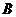 、
、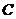 為△ABC的內角,
為△ABC的內角,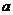 、
、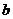 、
、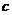 為角
為角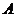 、
、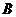 、
、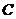 所對的邊.
所對的邊.
(Ⅰ)求角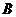 的大小;
的大小;
(Ⅱ) 若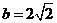 ,求△ABC的面積.
,求△ABC的面積.
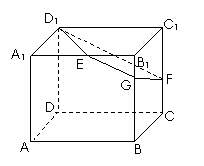
16. 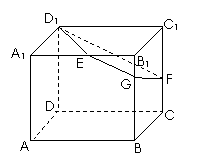 如圖,已知正方體
如圖,已知正方體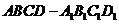 的棱長為2,E、F分別是
的棱長為2,E、F分別是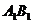 、
、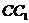 的中點,過
的中點,過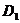 、E、F作平面
、E、F作平面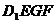 交
交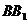 于G..
于G..
(1)求證: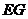 ∥
∥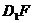 ;
;
(2)求正方體被平面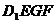 所截得的幾何體
所截得的幾何體
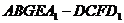 的體積.
的體積.
17.已知圓C: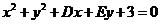 ,圓C關于直線
,圓C關于直線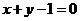 對稱,圓心在第二象限,半徑為
對稱,圓心在第二象限,半徑為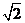
(Ⅰ)求圓C的方程;
(Ⅱ)已知不過原點的直線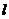 與圓C相切,且在x軸、y軸上的截距相等,求直線
與圓C相切,且在x軸、y軸上的截距相等,求直線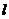 的方程。
的方程。
18. 設實數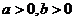 ,且滿足
,且滿足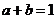
(1)求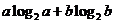 的最小值;
的最小值;
(2)設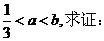 (
(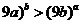
19.已知數列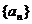 滿足:
滿足: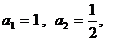 且
且
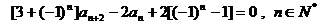 .
.
(Ⅰ)求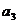 ,
,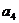 ,
,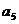 ,
,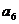 的值及數列
的值及數列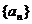 的通項公式;
的通項公式;
(Ⅱ)設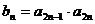 ,求數列
,求數列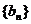 的前
的前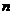 項和
項和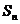 ;
;
20. 已知二次函數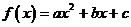 .
.
(1)若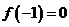 ,試判斷函數
,試判斷函數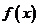 零點個數;
零點個數;
(2)若對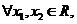 且
且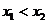 ,
,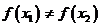 ,試證明
,試證明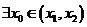 ,使
,使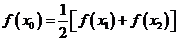 成立。
成立。
(3)是否存在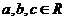 ,使
,使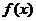 同時滿足以下條件①對
同時滿足以下條件①對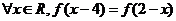 ,且
,且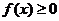 ;②對
;②對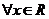 ,都有
,都有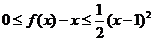 。若存在,求出
。若存在,求出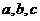 的值,若不存在,請說明理由。
的值,若不存在,請說明理由。
試題答案
一.填空題
1. 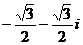 2. 0 3.
2. 0 3. 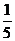 4.
4. 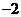 或
或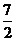 5.
5.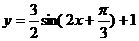
6. 0
7. 30 8.  9. 50 10.
9. 50 10. 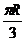
11. 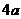 12.
12. 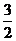 13、
13、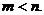 ; 14、
; 14、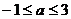 ;
;
二.解答題
15. 解:(Ⅰ)∵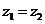 ∴
∴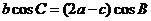 ----①,
----①,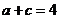 ----②
----②
由①得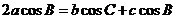 ------③
------③
在△ABC中,由正弦定理得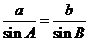 =
=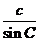 ,設
,設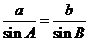
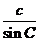 =
=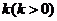
則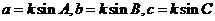 ,代入③得
,代入③得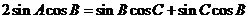
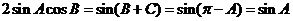
∵ 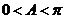 ∴
∴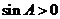 ∴
∴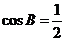 ,∵
,∵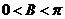 ∴
∴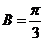
(Ⅱ) ∵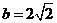 ,由余弦定理得
,由余弦定理得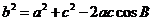
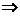
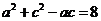 ,--④
,--④
由②得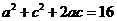 -⑤ 由④⑤得
-⑤ 由④⑤得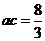 ,∴
,∴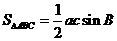 =
=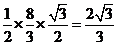 .
.
16. .(1)證明:在正方體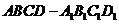 中,∵平面
中,∵平面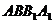 ∥平面
∥平面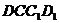
平面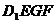
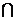 平面
平面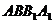
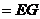 ,平面
,平面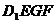
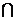 平面
平面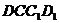
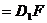
 ∴
∴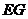 ∥
∥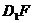 .
.
(2)解:設所求幾何體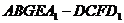 的體積為V,
的體積為V,
∵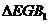 ~
~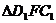 ,
,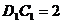 ,
,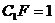 ,
,
∴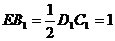 ,
,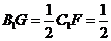 ,
,
∴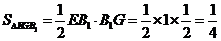 ,
,
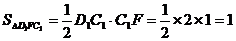
故V棱臺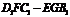
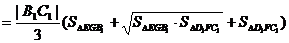
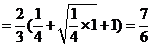
∴V=V正方體-V棱臺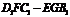
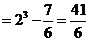 .
.
17. 解:(Ⅰ)由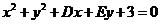 知圓心C的坐標為
知圓心C的坐標為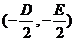
∵圓C關于直線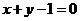 對稱
對稱
∴點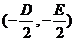 在直線
在直線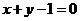 上
上
即D+E=-2,------------①且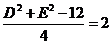 -----------------②
-----------------②
又∵圓心C在第二象限 ∴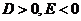
由①②解得D=2,E=-4
∴所求圓C的方程為: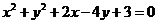
(Ⅱ)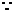 切線在兩坐標軸上的截距相等且不為零,設
切線在兩坐標軸上的截距相等且不為零,設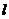 :
: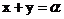
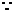 圓C:
圓C: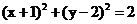
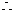 圓心
圓心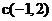 到切線的距離等于半徑
到切線的距離等于半徑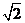 ,
,
即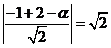
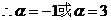 。
。
所求切線方程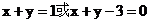
18. .解:(1)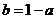 代入得
代入得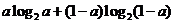
設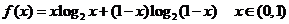
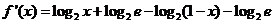
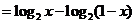 3分
3分
令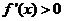 解得
解得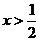
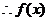 在
在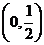 上單調遞減,在
上單調遞減,在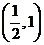 上單調遞增。
上單調遞增。
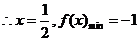 即原式的最小值為-1
即原式的最小值為-1
(2)要證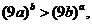 即證
即證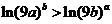
即證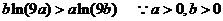
即證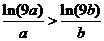
由已知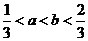 設
設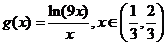
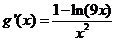
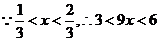
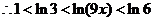
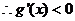
所以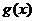 在
在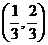 上單調遞減,
上單調遞減,
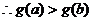
原不等式得證。
19.解:(Ⅰ)經計算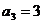 ,
,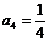 ,
,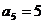 ,
,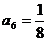 .
.
當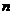 為奇數時,
為奇數時,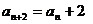 ,即數列
,即數列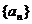 的奇數項成等差數列,
的奇數項成等差數列,
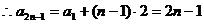 ;
;
當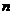 為偶數,
為偶數,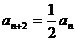 ,即數列
,即數列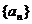 的偶數項成等比數列,
的偶數項成等比數列,
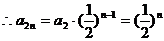 .
.
因此,數列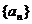 的通項公式為
的通項公式為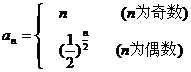 .
.
(Ⅱ)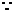
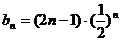 ,
,
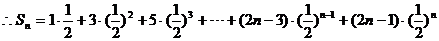 ……(1)
……(1)
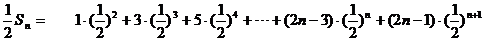 …(2)
…(2)
(1)、(2)兩式相減,
得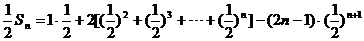
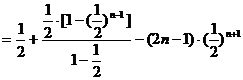
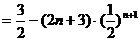 .
.
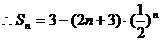 .
.
20. .解(1) 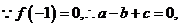
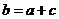
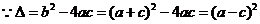 ,
,
當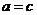 時
時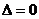 ,函數
,函數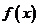 有一個零點;
有一個零點;
當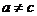 時,
時,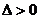 ,函數
,函數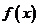 有兩個零點。
有兩個零點。
(2)令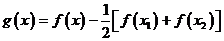 ,則
,則

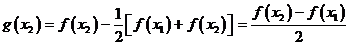 ,
,
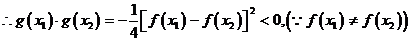
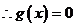 在
在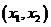 內必有一個實根。即
內必有一個實根。即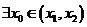 ,使
,使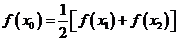 成立。
成立。
(3)
假設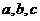 存在,由①知拋物線的對稱軸為x=-1,且
存在,由①知拋物線的對稱軸為x=-1,且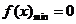
∴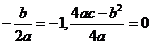
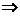
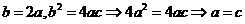
由②知對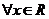 ,都有
,都有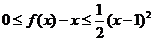
令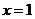 得
得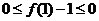
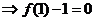
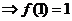
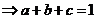
由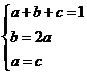 得
得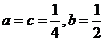 ,
,
當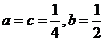 時,
時,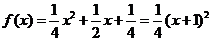 ,其頂點為(-1,0)滿足條件①,又
,其頂點為(-1,0)滿足條件①,又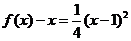
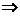 對
對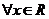 ,都有
,都有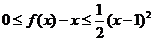 ,滿足條件②。
,滿足條件②。
∴存在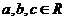 ,使
,使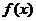 同時滿足條件①、②。
同時滿足條件①、②。
www.uz2rxb8d2.cn
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com