
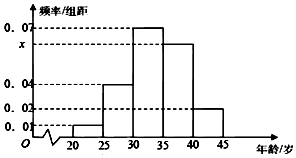
 為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].
為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].分析 (Ⅰ)根據小矩形的面積等于頻率,除[35,40)外的頻率和為0.70,即可得出.
(Ⅱ)用分層抽樣的方法,從中選取10名,則其中年齡“低于35歲”的人有6名,“年齡不低于35歲”的人有4名,故X的可能取值為0,1,2,3.利用超幾何分布列的計算公式及其數學期望計算公式即可得出.
解答 解:(Ⅰ)∵小矩形的面積等于頻率,∴除[35,40)外的頻率和為0.70,
∴$x=\frac{1-0.70}{5}=0.06$
500名志愿者中,年齡在[35,40)歲的人數為0.06×5×500=150(人)
(Ⅱ)用分層抽樣的方法,從中選取10名,則其中年齡“低于35歲”的人有6名,
“年齡不低于35歲”的人有4名,故X的可能取值為0,1,2,3.$P({X=0})=\frac{C_4^3}{{C_{10}^3}}=\frac{1}{30}$,$P({X=1})=\frac{C_6^1C_4^2}{{C_{10}^3}}=\frac{3}{10}$,$P({X=2})=\frac{C_6^2C_4^1}{{C_{10}^3}}=\frac{1}{2}$,$P({X=3})=\frac{C_6^3}{{C_{10}^3}}=\frac{1}{6}$.
故X的分布列為
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
點評 本題考查了頻率分布直方圖的性質、分層抽樣的方法、超幾何分布列的計算公式及其數學期望計算公式,考查了推理能力與計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 對任意的x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
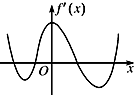
| A. | 無極大值點,有四個極小值點 | B. | 有三個極大值點,兩個極小值點 | ||
| C. | 有兩個極大值點,兩個極小值點 | D. | 有四個極大值點,無極小值點 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | a<c<b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com