
分析 (Ⅰ)由橢圓定義可知,點P的軌跡C是以N,F為焦點,長半軸長為2的橢圓,由此能求出曲線C的方程.
(Ⅱ)存在△AOB面積的最大值.由直線l過點E(-1,0),設直線l的方程為 x=my-1,聯立橢圓方程,整理得(m2+4)y2-2my-3=0.由△=(2m)2+12(m2+4)>0.設A(x1,y1),B(x2,y2).解得y1=$\frac{m+2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$,y2=$\frac{m-2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.再換元,結合函數的單調性,由此能求出S△AOB的最大值.
解答 解:( I)易知點F($\sqrt{3}$,0)在圓M:(x+$\sqrt{3}$)2+y2=16內,所以圓N內切于圓M,又圓M的半徑為4,所以|NM|+|NF|=4>2$\sqrt{3}$=|FM|,所以點N的軌跡C為橢圓,且2a=4,c=$\sqrt{3}$,所以b=1,
所以軌跡C的方程為$\frac{{x}^{2}}{4}+{y}^{2}$=1 (4分)
(Ⅱ)存在△AOB面積的最大值.…(6分)
因為直線l過點E(-1,0),設直線l的方程為 x=my-1或y=0(舍).
聯立橢圓方程,整理得 (m2+4)y2-2my-3=0.…(7分)
由△=(2m)2+12(m2+4)>0.
設A(x1,y1),B(x2,y2).
解得y1=$\frac{m+2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$,y2=$\frac{m-2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
則|y2-y1|=$\frac{4\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
∴S△AOB=$\frac{1}{2}$|OE||y2-y1|=$\frac{2}{\sqrt{{m}^{2}+3}+\frac{1}{\sqrt{{m}^{2}+3}}}$ …(10分)
設g(t)=t+$\frac{1}{t}$,t=$\sqrt{{m}^{2}+3}$,t≥$\sqrt{3}$.
則g(t)在區間[$\sqrt{3}$,+∞)上為增函數.
所以g(t)≥$\frac{4\sqrt{3}}{3}$.
所以S△AOB≤$\frac{\sqrt{3}}{2}$,
當且僅當m=0時取等號,所以S△AOB的最大值為$\frac{\sqrt{3}}{2}$.…(13分)
點評 本題考查曲線的軌跡方程的求法,考查三角形的面積的最大值的求法,解題時要認真審題,注意等價轉化思想的合理運用.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
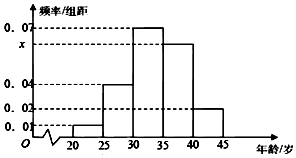 為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].
為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 42 | B. | 44 | C. | 46 | D. | 48 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n=45,p=$\frac{2}{3}$ | B. | n=45,p=$\frac{1}{3}$ | C. | n=90,p=$\frac{1}{3}$ | D. | n=90,p=$\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若x=1,則x2+x-2=0”的否命題是假命題 | |
| B. | 命題“存在一個實數x,使不等式x2-3x+4<0成立”為真命題 | |
| C. | 命題“若x2-3x+2=0,則x=1”的逆否命題為“若x≠1,則x2-3x+2≠0” | |
| D. | 過點(0,2)與拋物線y2=8x只有一個公共點的直線有3條 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com