
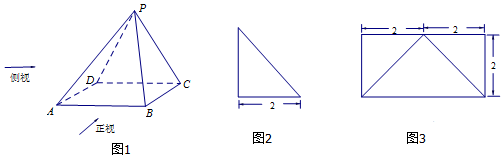
分析 (1)根據三視圖形狀可得側面PDC⊥平面ABCD,結合矩形ABCD中AD⊥CD,由面面垂直的性質得AD⊥側面PDC.再根據線面垂直的性質,結合PC?側面PDC可證出AD⊥PC;
(2)過E作EF⊥AB,垂足為F,連接PF,分別求出側面積,即得四棱錐P-ABCD的側面積.
解答 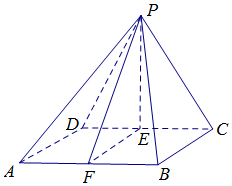 (1)證明:依題意,可知點P在平面ABCD上的正射影是線段CD的中點E,連接PE,
(1)證明:依題意,可知點P在平面ABCD上的正射影是線段CD的中點E,連接PE,
則PE⊥平面ABCD.…(1分)
∵AD?平面ABCD,
∴AD⊥PE.…(2分)
∵AD⊥CD,CD∩PE=E,CD?平面PCD,PE?平面PCD,
∴AD⊥平面PCD.…(4分)
∵PC?平面PCD,
∴AD⊥PC.…(5分)
(2)解:依題意,在等腰三角形PCD中,PC=PD=3,DE=EC=2,
在Rt△PED中,$PE=\sqrt{P{D^2}-D{E^2}}=\sqrt{5}$,…(6分)
過E作EF⊥AB,垂足為F,連接PF,
∵PE⊥平面ABCD,AB?平面ABCD,
∴AB⊥PE.
∵EF?平面PEF,PE?平面PEF,EF∩PE=E,
∴AB⊥平面PEF.
∵PF?平面PEF,
∴AB⊥PF.
依題意得EF=AD=2.
在Rt△PEF中,$PF=\sqrt{P{E^2}+E{F^2}}=3$,…(9分)
∴四棱錐P-ABCD的側面積
$\begin{array}{l}{S_{△PAB}}+{S_{△PBC}}+{S_{△PCD}}+{S_{△PAD}}=\frac{1}{2}×4×3+2×\frac{1}{2}×2×3+\frac{1}{2}×4×\sqrt{5}\\=12+2\sqrt{5}\end{array}$.…(12分)
點評 本題給出三視圖,要求我們證明線線垂直并求側面三角形的面積,著重考查了三視圖求面積和面面垂直、線面垂直的性質定理等知識,屬于中檔題.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | 2 | D. | 5$\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①②④ | B. | ②③⑤ | C. | ①③④ | D. | ①②⑤ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
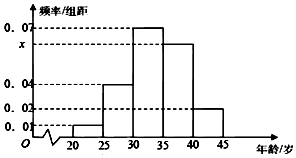 為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].
為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:[20,25],[25,30],[30,35],[35,40],[40,45].查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com