
分析 (1)利用零點分段法,可將函數解析式化為分段函數,進而結合一次函數的圖象和性質,得到函數的圖象;
(2)數形結合,可得函數的值域、單調區間;
(3)若對任意x∈R,不等式|2x-1|≥a+x恒成立,則a≤|2x-1|-x的最小值.
解答 解:(1)∵函數f(x)=|2x-1|-x=$\left\{\begin{array}{l}-3x+1,x<\frac{1}{2}\\ x-1,x≥\frac{1}{2}\end{array}\right.$,
函數的圖象如下圖所示: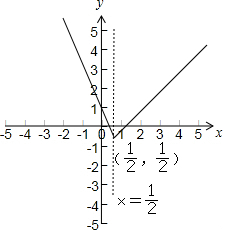
(2)由圖可得:函數的值域為:[-$\frac{1}{2}$,+∞);
單調減區間為:為:(-∞,$\frac{1}{2}$],單調增區間為:[$\frac{1}{2}$,+∞);
(3)若對任意x∈R,不等式|2x-1|≥a+x恒成立,
則a≤|2x-1|-x恒成立,
即a≤-$\frac{1}{2}$.
點評 本題考查的知識點是分段函數的應用,函數的圖象,函數的單調性,函數的值域,函數恒成立問題,難度中檔.


 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 12 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4032}{2016}$ | B. | $\frac{4034}{2017}$ | C. | $\frac{4032}{2018}$ | D. | $\frac{4034}{2018}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 用小正方體搭一個幾何體,使得它的正視圖和俯視圖如圖所示,這樣的幾何體只有一種嗎?若不是,則這種幾何體最少需要多少個小正方體?最多需要多少個小正方體?
用小正方體搭一個幾何體,使得它的正視圖和俯視圖如圖所示,這樣的幾何體只有一種嗎?若不是,則這種幾何體最少需要多少個小正方體?最多需要多少個小正方體?查看答案和解析>>
科目:高中數學 來源: 題型:填空題
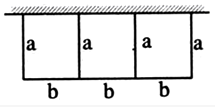
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | (1,+∞) | C. | (3,+∞) | D. | [-$\frac{9}{4}$,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com