
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ-$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z | ||
| C. | [kπ-$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ+$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z |
分析 由題意求得周期,再由周期公式求得ω,結合函數對稱軸求出φ,則函數f(x)的解析式可求,再由函數的圖象平移求得g(x),利用復合函數的單調性求g(x)的單調遞減區間.
解答 解:由圖象上相鄰最高點的距離為π,的T=$\frac{2π}{ω}$=π,則ω=2.
∴f(x)=$\sqrt{3}$sin(2x+φ),
又圖象關于直線x=$\frac{π}{3}$對稱,
∴2×$\frac{π}{3}+$φ=$\frac{π}{2}+kπ$,k∈Z.
∴φ=$-\frac{π}{6}+kπ$,k∈Z.
∵-$\frac{π}{2}$≤φ<$\frac{π}{2}$,
∴k=0時,φ=-$\frac{π}{6}$.
則f(x)=$\sqrt{3}$sin(2x$-\frac{π}{6}$),
函數y=f(x)的圖象向右平移$\frac{π}{12}$個單位后,
得到y=g(x)=f(x$-\frac{π}{12}$)=$\sqrt{3}$sin[2(x$-\frac{π}{12}$)$-\frac{π}{6}$]=$\sqrt{3}$sin(2x$-\frac{π}{3}$).
由$\frac{π}{2}+2kπ≤2x-\frac{π}{3}≤\frac{3π}{2}+2kπ$,得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$,k∈Z.
∴g(x)的單調遞減區間為[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z.
故選:A.
點評 本題考查三角函數的圖象變換,考查y=Asin(ωx+φ)型函數的圖象和性質,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
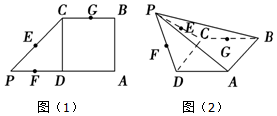 在如圖(1)的平面圖形中,ABCD為正方形,CDP為等腰直角三角形,E、F、G分別是PC、PD、CB的中點,將△PCD沿CD折起,得到四棱錐P-ABCD如圖(2).
在如圖(1)的平面圖形中,ABCD為正方形,CDP為等腰直角三角形,E、F、G分別是PC、PD、CB的中點,將△PCD沿CD折起,得到四棱錐P-ABCD如圖(2).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{64}{15}$ | C. | $\frac{16}{19}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com