
分析 由題意作出三角函數線,通過三角形的面積以及扇形面積的大小比較可得.
解答 解:在直角坐標系中結合單位圓作出銳角α的正弦線和正切線,
如圖所示;
由圖可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,
S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,
S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,
且S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,
即sinα<α<tanα.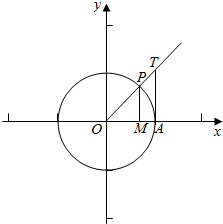
點評 本題考查了三角函數線,也考查了數形結合與轉化思想應用問題,屬中檔題.


 優學名師名題系列答案
優學名師名題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {(λ,μ)|λ-μ=2} | B. | {(λ,μ)|λ+μ=2} | C. | {(λ,μ)|λ2-μ2=2} | D. | {(λ,μ)|λ2+μ2=2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 喜愛 | 不喜愛 | 合計 | |
| 男同學 | 24 | 6 | 30 |
| 女同學 | 6 | 14 | 20 |
| 合計 | 30 | 20 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
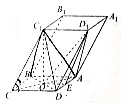 如圖所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,線段AC與BD的交點為O.
如圖所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,線段AC與BD的交點為O.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | ($\frac{4}{3}$,0) | ||
| C. | (-∞,0)∪($\frac{4}{3}$,0) | D. | (-∞,-$\frac{1}{3}$)∪(-$\frac{1}{3}$,0)∪($\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {1,2,5} | D. | {2,5} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ-$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z | ||
| C. | [kπ-$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ+$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com