Question

11．若O為△ABC所在平面內任一點，且滿足$\overrightarrow{BC}•（\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}）=0$，則△ABC的形狀為（　　）

• A． 正三角形
• B． 直角三角形
• C． 等腰三角形
• D． 等腰直角三角形

Answer 1

分析 取BC的中點D，根據平面向量的線性運算計算$\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}$=2$\overrightarrow{AD}$，從而BC⊥AD，于是AB=AC．

解答 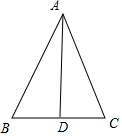解：取BC中點D，連接AD，
則$\overrightarrow{OB}+\overrightarrow{OC}$=2$\overrightarrow{OD}$，
又$\overrightarrow{OD}-\overrightarrow{OA}$=$\overrightarrow{AD}$，
∴$\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}$=2$\overrightarrow{OD}$-2$\overrightarrow{OA}$=2$\overrightarrow{AD}$，
∵$\overrightarrow{BC}•（\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}）$=0，
$2\overrightarrow{BC}•\overrightarrow{AD}$=0，
∴$\overrightarrow{BC}⊥\overrightarrow{AD}$；
∴AB=AC；
∴△ABC的形狀是等腰三角形．
故選：C．

點評 本題考查了平面向量的線性運算，數量積運算，屬于中檔題．