
分析 (1)根據題意由余弦定理a2=b2+c2-2bccosA,可求得cosA的值,再利用A為△ABC中的角,即可求得A.
(2)利用等差數列的定義即可求出數列{an}的通項公式,利用裂項求出和,求出Sn,由n∈N+和Sn單調性可求出Sn的取值范圍.
解答 解:(1)∵b2+c2=a2+bc,
∴$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,
又∵A∈(0,π),
∴$A=\frac{π}{3}$.
(2)由(1)知${a_1}=2cosA=2cos\frac{π}{3}=1$,
設等差數列{an}的公差為d,
∵a5=a1+(5-1)d=9,
∴d=2,
∴an=1+2(n-1)=2n-1,
∴$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({2n-1})({2n+1})}}=\frac{1}{2}({\frac{1}{{({2n-1})}}\frac{1}{{({2n+1})}}})$,
∴${S_n}=\frac{1}{2}({1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1}})=\frac{1}{2}({1-\frac{1}{2n+1}})<\frac{1}{2}$.
顯然$\frac{1}{2n+1}$為遞減數列,
故$1-\frac{1}{2n+1}$為遞增數列,
故${S_n}=\frac{1}{2}({1-\frac{1}{2n+1}})$的最小值為${S_1}=\frac{1}{3}$,
故$\frac{1}{3}≤{S_n}<\frac{1}{2}$.
點評 本題考查余弦定理和等差數列的通項公式和裂項求和,還考查了函數的單調性,裂項求和是最重要的數列求和方法這一.屬于中檔題.


科目:高中數學 來源: 題型:選擇題
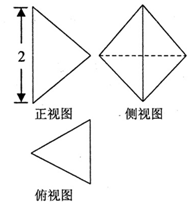 某幾何體的三視圖如圖所示,其俯視圖是邊長為1的正三角形,側視圖是菱形,則這個幾何體的體積為( )
某幾何體的三視圖如圖所示,其俯視圖是邊長為1的正三角形,側視圖是菱形,則這個幾何體的體積為( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 45°,$\frac{{4\sqrt{2}}}{3}$ | B. | 30°,$\frac{{4\sqrt{2}}}{3}$ | C. | 60°,$\frac{{2\sqrt{2}}}{3}$ | D. | 75°,$\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (5,8) | B. | (8,+∞) | C. | ($\frac{13}{2}$,8) | D. | (5,$\frac{13}{2}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com