
分析 當m=0時,不等式顯然成立;當m≠0時,根據二次函數圖象的性質得到m的取值范圍.兩者取并集即可得到m的取值范圍.
解答 解:當m=0時,mx2-2mx-3=-3<0,不等式成立;
設y=mx2-2mx-3,當m≠0時函數y為二次函數,y要恒小于0,拋物線開口向下且與x軸沒有交點,
即要m<0且△<0,
得到:$\left\{\begin{array}{l}{m<0}\\{4{m}^{2}+12m<0}\end{array}\right.$解得-3<m<0.
綜上得到-3<m≤0
故答案為:(-3,0].
點評 本題以不等式恒成立為平臺,考查學生會求一元二次不等式的解集.同時要求學生把二次函數的圖象性質與一元二次不等式結合起來解決數學問題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
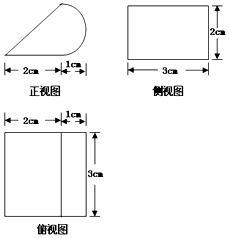
| A. | (19+π)cm2 | B. | (22+4π)cm2 | C. | (10+6$\sqrt{2}$+4π)cm2 | D. | (13+6$\sqrt{2}$+4π)cm2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 流量超過1000M | 流量沒有超過1000M | 合計 | |
| 男 | 20 | 25 | 45 |
| 女 | 40 | 15 | 55 |
| 合計 | 60 | 40 | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com