
分析 根據函數(shù)中存在“倍值區(qū)間”的兩個條件:①f(x)在[m,n]上是單調函數(shù),②$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.或\left\{\begin{array}{l}{f(m)=2n}\\{f(n)=2m}\end{array}\right.$,對四個函數(shù)分別研究,從而確定是否存在“倍值區(qū)間”.
解答 解:函數(shù)中存在“倍值區(qū)間”的兩個條件:①f(x)在[m,n]上是單調函數(shù),②$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.或\left\{\begin{array}{l}{f(m)=2n}\\{f(n)=2m}\end{array}\right.$,
對于①,f(x)=x2(x≥0)在[0.+∞)上單增調,若存在“倍值區(qū)間[m,n],⇒f(m)=2m,f(n)=2n⇒$\left\{\begin{array}{l}{{m}^{2}=2m}\\{{n}^{2}=2n}\end{array}\right.$⇒$\left\{\begin{array}{l}{m=0}\\{n=2}\end{array}\right.$,∴f(x)=x2(x≥0),存在“倍值區(qū)間”[0,2];
對于②,f(x)=ex(x∈R)在R上單增調,構建函數(shù)g(x)=ex-2x,∴g′(x)=ex-2,
∴函數(shù)在(-∞,ln2)上單調減,在(ln2,+∞)上單調增,
∴函數(shù)在x=ln2處取得極小值,且為最小值.
∵g(ln2)=2-ln2,∴g(x)>0,∴ex-2x=0無解,故函數(shù)不存在“倍值區(qū)間“;
對于③,f(x)=$\frac{4x}{{x}^{2}+1}=\frac{4}{x+\frac{1}{x}}$(x≠0),故f(x)在區(qū)間[0,1]上單調遞增,在區(qū)間[1,+∞)上單調遞減,
f(0)=0.f(1)=2∴存在“倍值區(qū)間”[0,1];
對于④,f(x)=log2(2x-$\frac{1}{8}$),則函數(shù)在定義域內為單調增函數(shù),若存在“倍值區(qū)間”[m,n],
∴m,n是方程log2(2x-$\frac{1}{8}$)=2x的兩個根,
∴m,n是方程22x-2x+$\frac{1}{8}$=0的兩個根,
由于該方程有兩個不等的正根,故存在“倍值區(qū)間”[m,n];
綜上知,所給函數(shù)中存在“倍值區(qū)間”的有①③④.
故答案為:①③④.
點評 本題考查新定義,考查學生分析解決問題的能力,涉及知識點較多,計算量大,屬于難題..


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $-\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $-\frac{12}{13}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
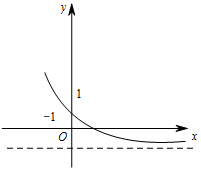
| A. | 0<a<1,-1<b<0 | B. | 0<a<1,0<b<1 | C. | 1<a,-1<b<0 | D. | 1<a,0<b<1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
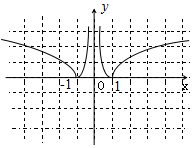 已知函數(shù)f(x)是定義在{x|x≠0}上的偶函數(shù),且當x>0時,f(x)=log2x.
已知函數(shù)f(x)是定義在{x|x≠0}上的偶函數(shù),且當x>0時,f(x)=log2x.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}$=1 | C. | $\frac{{x}^{2}}{80}-\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{80}$=1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com