
分析 (1)利用奇函數的定義求解即可:即f(-x)+f(x)=0.
(2)求函數的定義域,利用定法證明其單調性.
(3)對函數進行化簡,分離常數法,即可得到值域.
解答 解:(1)由題意:函數f(x)=$\frac{1-{2}^{x}}{a+{2}^{x+1}}$是奇函數.
∴f(-x)+f(x)=0.
即:$\frac{1-{2}^{-x}}{a+{2}^{1-x}}+$$\frac{1-{2}^{x}}{a+{2}^{x+1}}$=0
化簡整理得:$\frac{{2}^{x}-1}{a•{2}^{x}+2}+\frac{1-{2}^{x}}{a+2•{2}^{x}}$=0
可得:a•2x+2=a+2•2x
解得:a=2.
所以實數a的值為2.
(2)由(1)得f(x)=$\frac{1-{2}^{x}}{2(1+{2}^{x})}$,其定義域為R.
函數f(x)在定義域R上單調減函數.證明如下:
設x1<x2,那么:f(x1)-f(x2)=$\frac{1-{2}^{{x}_{1}}}{2(1+{2}^{{x}_{1}})}-\frac{1-{2}^{{x}_{2}}}{2(1+{2}^{{x}_{2}})}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$,
∵x1<x2,
∴${2}^{{x}_{2}}-{2}^{{x}_{1}}>0$,
故得f(x1)-f(x2)>0.
所以函數f(x)在定義域R上單調減函數.
(3)由(1)可得f(x)=$\frac{1-{2}^{x}}{2(1+{2}^{x})}$=$\frac{2-(1+{2}^{x})}{2(1+{2}^{x})}$=$-\frac{1}{2}+\frac{1}{1+{2}^{x}}$.
∵$\frac{1}{1+{2}^{x}}≠0$
∴f(x)$≠-\frac{1}{2}$,
所以函數f(x)的值域為(-∞,$-\frac{1}{2}$)∪($-\frac{1}{2}$,+∞).
點評 本題考查了奇函數的運用能力和單調性的定義的運用,分離常數法求解值域.屬于基礎題.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | {a|a≥4} | B. | {a|a>4或a=0} | C. | {a|0≤a≤4} | D. | {a|a≥4或a=0} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知△OCB中,A是BC邊的中點,D是OB邊上靠近點B的三等分點,DC與OA相交于點E,DE:DC=2:5,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
如圖,已知△OCB中,A是BC邊的中點,D是OB邊上靠近點B的三等分點,DC與OA相交于點E,DE:DC=2:5,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
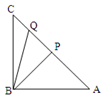 如圖,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,點P在線段AC上,若點Q在線段PC上,且∠PBQ=30°,則△BPQ的面積的最小值為8-4$\sqrt{3}$.
如圖,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,點P在線段AC上,若點Q在線段PC上,且∠PBQ=30°,則△BPQ的面積的最小值為8-4$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
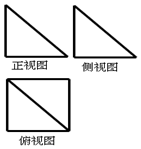 一個幾何體的三視圖如圖所示,其中正視圖和側視圖是腰長為2的兩個全等的等腰直角三角形,則該幾何體的外接球的表面積是( )
一個幾何體的三視圖如圖所示,其中正視圖和側視圖是腰長為2的兩個全等的等腰直角三角形,則該幾何體的外接球的表面積是( )| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$π | C. | 12π | D. | $\frac{8\sqrt{3}}{3}$π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com