Question

7．如圖，M、N分別是AB、AC的一個三等分點，且$\overrightarrow{MN}$=λ（$\overrightarrow{AC}$-$\overrightarrow{AB}$）成立，則λ=（　　）

• A． $\frac{1}{2}$
• B． ±$\frac{1}{3}$
• C． $\frac{2}{3}$
• D． $\frac{1}{3}$

Answer 1

分析 根據圖象和向量的數乘、減法運算，表示出$\overrightarrow{MN}$，即可求出λ的值．

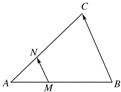
解答 解：∵M、N分別是AB、AC的一個三等分點，
∴$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}$，$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$，
∴$\overrightarrow{MN}$=$\overrightarrow{AN}-\overrightarrow{AM}$=$\frac{1}{3}$（$\overrightarrow{AC}$-$\overrightarrow{AB}$），
又$\overrightarrow{MN}$=λ（$\overrightarrow{AC}$-$\overrightarrow{AB}$）成立，即λ=$\frac{1}{3}$，
故選：D．

點評 本題考查了向量的基本定理，以及向量的數乘、減法運算的應用，屬于基礎題．