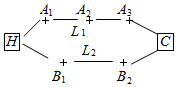Question

8．如圖，李先生家住H小區，他工作在C處科技園區，從家開車到公司上班路上有L₁、L₂兩條路線，L₁路線上有A₁、A₂、A₃三個路口，各路口遇到紅燈的概率均為$\frac{1}{2}$；L₂路線上有B₁、B₂兩個路口，各路口遇到紅燈的概率依次為$\frac{3}{4}$，$\frac{3}{5}$．
（1）若走L₂路線，求遇到紅燈次數X的分布列和數學期望；
（2）按照“平均遇到紅燈次數最少”的要求，請你幫助李先生從上述兩條路線中選擇一條最好的上班路線，并說明理由．

Answer 1

分析 （1）走L₂路線，遇到紅燈次數X的取值為0，1，2．利用相互獨立事件、互斥事件的概率計算公式即可得出概率、分布列及其數學期望．
（2）走L₁路線，遇到紅燈次數ξ～B$（3，\frac{1}{2}）$，可得Eξ．比較Eξ與EX的大小關系即可得出結論．

解答 解：（1）走L₂路線，遇到紅燈次數X的取值為0，1，2．
P（X=0）=$（1-\frac{3}{4}）×（1-\frac{3}{5}）$=$\frac{1}{10}$，P（X=1）=$（1-\frac{3}{4}）$×$\frac{3}{5}$+$\frac{3}{4}$×$（1-\frac{3}{5}）$=$\frac{9}{20}$，P（X=2）=$\frac{3}{4}×\frac{3}{5}$=$\frac{9}{20}$．
∴X分布列為：

X	0	1	2
P	$\frac{1}{10}$	$\frac{9}{20}$	$\frac{9}{20}$

數學期望EX=0×$\frac{1}{10}$+1×$\frac{9}{20}$+2×$\frac{9}{20}$=$\frac{27}{20}$．
（2）走L₁路線，遇到紅燈次數ξ～B$（3，\frac{1}{2}）$，則Eξ=$3×\frac{1}{2}$=$\frac{3}{2}$．
∴Eξ＞EX．
因此李先生從上述兩條路線中選擇L₂的路線上班．

點評 本題考查了相互獨立事件、互斥事件的概率計算公式、二項分布列的計算與數學期望，考查了推理能力與計算能力，屬于中檔題．