
| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 由題意可知f(x)在兩段上均為增函數,且f(x)在(0,+∞)上的最小值大于或等于f(0),作出|f(x)|和y=x+1的圖象,根據交點個數判斷3a與2的大小關系,列出不等式組解出.
解答 解:∵f(x)是R上的單調遞增函數,
∴y=x2+(4a-1)x+3a-1在(0,+∞)上單調遞增,y=($\frac{1}{a}$)x-1在(-∞,0]上單調遞增,
且f(x)在(0,+∞)上的最小值大于或等于f(0).
即$\left\{\begin{array}{l}{\frac{1}{a}>1}\\{\frac{1-4a}{2}≤0}\\{3a-1≥0}\end{array}\right.$解得$\frac{1}{3}≤a<1$,
作出y=|f(x)|和y=x+1的函數草圖如圖所示:
由圖象可知|f(x)|=x+1在(-∞,0)上有且只有一解,
∵|f(x)|=x+1恰有兩個不相等的實數解,
∴x2+(4a-1)x+3a-1=x+1在(0,+∞)上只有1解,
即x2+(4a-2)x+3a-2=0在(0,+∞)上只有1解,
$\left\{\begin{array}{l}{△=(4a-2)^{2}-4(3a-2)=0}\\{-\frac{4a-2}{2}>0}\end{array}\right.$或$\left\{\begin{array}{l}{△=(4a-2)^{2}-4(3a-2)>0}\\{3a-2<0}\end{array}\right.$
解得a$<\frac{2}{3}$.
綜上,a的取值范圍是:[$\frac{1}{3}$,$\frac{2}{3}$),
故選:B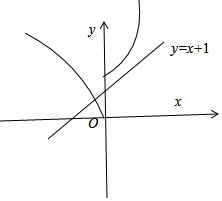
點評 本題考查了分段函數的單調性,函數零點的個數判斷,結合函數圖象判斷端點值的大小是關鍵,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
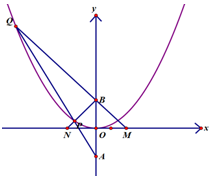 已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$.
已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | $\hat a>0,\hat b>0$ | B. | $\hat a>0,\hat b<0$ | C. | $\hat a<0,\hat b>0$ | D. | $\hat a<0,\hat b<0$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 10 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
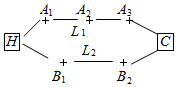 如圖,李先生家住H小區,他工作在C處科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為$\frac{1}{2}$;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為$\frac{3}{4}$,$\frac{3}{5}$.
如圖,李先生家住H小區,他工作在C處科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為$\frac{1}{2}$;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為$\frac{3}{4}$,$\frac{3}{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com