
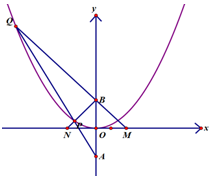
 已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$.
已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$. 分析 設PQ:y=kx-a,與拋物線方程x2=2py聯立,設P(x1,y1),Q(x2,y2),利用韋達定理,表示直線的斜率,通過kBP=-kBQ,kBP•kBQ=-3.求解即可.
解答 解:設PQ:y=kx-a,與拋物線方程x2=2py聯立得:x2-2pkx+2pa=0,
設P(x1,y1),Q(x2,y2),則有:x1+x2=2pk,x1x2=2pa,
${k_{BP}}+{k_{BQ}}=\frac{{{y_1}-a}}{x_1}+\frac{{{y_2}-a}}{x_2}=\frac{{2k{x_1}{x_2}-2a({x_1}+{x_2})}}{{{x_1}{x_2}}}=0$,
所以:kBP=-kBQ而:kBP•kBQ=-3.從而${k_{BP}}=\sqrt{3},{k_{BQ}}=-\sqrt{3}$,
從而得$∠NBM=\frac{π}{3},∠PBQ=\frac{2π}{3}$.
故答案為:$\frac{2π}{3}$.
點評 本題考查直線與拋物線的位置關系的應用,考查轉化思想以及計算能力.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:選擇題
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 在△ABC中,D、E分別是AB、AC的中點,M是直線DE上的動點.若△ABC的面積為2,則$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值為2$\sqrt{3}$.
在△ABC中,D、E分別是AB、AC的中點,M是直線DE上的動點.若△ABC的面積為2,則$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值為2$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com