
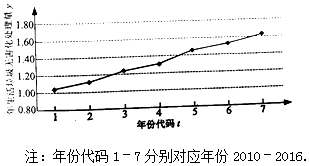
分析 (Ⅰ)由折線圖中數據和附注中參考數據,計算相關系數,根據相關系數的值得出結論;
(Ⅱ)計算回歸系數,寫出y關于t的回歸方程;將2018年對應的t值代入回歸方程,計算對應的函數值即可.
解答 解:(Ⅰ)由折線圖中數據和附注中參考數據得$\overline t=4$,
$\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}=28$,
$\sqrt{\sum_{i=1}^7{{{({y_i}-\overline y)}^2}}}=0.55$,
$\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}=\sum_{i=1}^7{{t_i}{y_i}-\overline t\sum_{i=1}^7{y_i}}=40.17-4×9.32=2.89$,
所以相關系數為$r≈\frac{2.89}{0.55×2×2.646}≈0.99$;…(4分)
因為y與t的相關系數近似為0.99,
說明y與t的線性相關程度相當高,從而可以用線性回歸模型擬合y與t的關系;…(6分)
(Ⅱ)由$\overline y=\frac{9.32}{7}≈1.331$及(Ⅰ)得,
$\hat b=\frac{{\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}=\frac{2.89}{28}≈0.103$,
$\hat a=\overline y-\hat b\overline t≈1.331-0.103×4≈0.92$;
所以,y關于t的回歸方程為:$\hat y=0.92+0.10t$;…(10分)
將2018年對應的t=9代入回歸方程得:
$\hat y=0.92+0.10×9=1.82$;
所以預測2016年我國生活垃圾無害化處理量將約1.82億噸…(12分)
點評 本題考查了相關系數與回歸直線方程的求法和應用問題,是中檔題.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
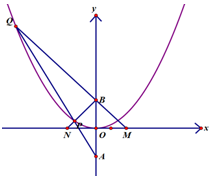 已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$.
已知拋物線的方程為x2=2py(p>0),過點A(0,-a)(a>0)作直線l與拋物線相交于P,Q兩點,點B的坐標為(0,a),連接BP,BQ.且QB,QP與x軸分別交于M,N兩點,如果QB的斜率與PB的斜率之積為-3,則∠PBQ=$\frac{2π}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | $\hat a>0,\hat b>0$ | B. | $\hat a>0,\hat b<0$ | C. | $\hat a<0,\hat b>0$ | D. | $\hat a<0,\hat b<0$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
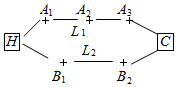 如圖,李先生家住H小區,他工作在C處科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為$\frac{1}{2}$;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為$\frac{3}{4}$,$\frac{3}{5}$.
如圖,李先生家住H小區,他工作在C處科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為$\frac{1}{2}$;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為$\frac{3}{4}$,$\frac{3}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com