
分析 由兩條直線垂直,可得:(2sinθ-1)+2$\sqrt{3}$cosθ=0,化簡得:sin(θ+$\frac{π}{3}$)=$\frac{1}{4}$,利用誘導公式即可計算得解.
解答 解:∵直線l1:(2sinθ-1)x+2cosθ•y+1=0,l2:x+$\sqrt{3}$y-3=0,
∴由l1⊥l2,得:(2sinθ-1)+2$\sqrt{3}$cosθ=0,
∴化簡得:sin(θ+$\frac{π}{3}$)=$\frac{1}{4}$,
∴$cos(θ-\frac{π}{6})=cos[(θ+\frac{π}{3})-\frac{π}{2}]=sin(θ+\frac{π}{3})=\frac{1}{4}$,
故答案為:$\frac{1}{4}$.
點評 本題考查直線的垂直關系,三角函數恒等變換的應用,考查了計算能力和轉化思想,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{8}$ | B. | $-\frac{7}{8}$ | C. | $-\frac{5}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
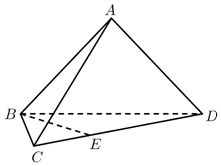 如圖,在三棱錐A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,點E在CD上,DE=2EC.
如圖,在三棱錐A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,點E在CD上,DE=2EC.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-3,1) | B. | (-1,3) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
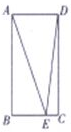 在如圖所示的矩形ABCD中,AB=4,AD=2,E為線段BC上的點,則$\overrightarrow{AE}•\overrightarrow{DE}$的最小值為( )
在如圖所示的矩形ABCD中,AB=4,AD=2,E為線段BC上的點,則$\overrightarrow{AE}•\overrightarrow{DE}$的最小值為( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 在△ABC中,D、E分別是AB、AC的中點,M是直線DE上的動點.若△ABC的面積為2,則$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值為2$\sqrt{3}$.
在△ABC中,D、E分別是AB、AC的中點,M是直線DE上的動點.若△ABC的面積為2,則$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值為2$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com