
| A. | $[{\frac{7π}{12},\frac{13π}{12}}]$ | B. | $[{\frac{π}{12},\frac{7π}{12}}]$ | C. | $[{-\frac{π}{2},\frac{π}{2}}]$ | D. | $[{-\frac{5π}{6},\frac{π}{6}}]$ |
分析 利用誘導公式化簡函數(shù)的解析式,再利用余弦函數(shù)的單調(diào)性,求得f(x)的一個增區(qū)間.
解答 解:對于函數(shù)$f(x)=3sin({\frac{2π}{3}-2x})$=3cos($\frac{π}{6}$-2x)=3cos(2x-$\frac{π}{6}$),
令2kπ-π≤2x-$\frac{π}{6}$≤2kπ,求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,可得函數(shù)的增區(qū)間為[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈Z,
令k=1,可得選項A正確,
故選:A.
點評 本題主要考查誘導公式、余弦函數(shù)的單調(diào)性,屬于基礎(chǔ)題.


科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
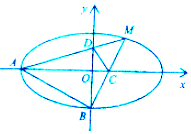 已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{3}}}{2}$,過橢圓的焦點且與長軸垂直的弦長為1.
已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{3}}}{2}$,過橢圓的焦點且與長軸垂直的弦長為1.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{10}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{19}$ | D. | $\frac{20}{19}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
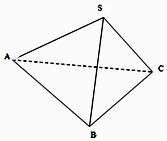 如圖,已知三棱錐S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,則二面角S-AB-C的平面角的大小為( )
如圖,已知三棱錐S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,則二面角S-AB-C的平面角的大小為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com