Question

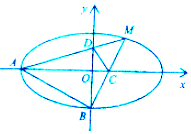
5．已知橢圓$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的離心率為$\frac{{\sqrt{3}}}{2}$，過橢圓的焦點(diǎn)且與長軸垂直的弦長為1．
（1）求橢圓C的方程；
（2）設(shè)點(diǎn)M為橢圓上位于第一象限內(nèi)一動(dòng)點(diǎn)，A，B分別為橢圓的左頂點(diǎn)和下頂點(diǎn)，直線MB與x軸交于點(diǎn)C，直線MA與軸交于點(diǎn)D，求證：四邊形ABCD的面積為定值．

Answer 1

分析 （1）由橢圓的離心率為$\frac{{\sqrt{3}}}{2}$，過橢圓的焦點(diǎn)且與長軸垂直的弦長為1，列出方程組，求出a，b，由此能求出橢圓C的方程．
（2）設(shè)M（m，n），（m＞0，n＞0），則m²+4n²=4，從而直線BM的方程為y=$\frac{n+1}{m}x-1$，進(jìn)而${x}_{C}=\frac{m}{n+1}$，同理，得${y}_{D}=\frac{2n}{m+2}$，進(jìn)而${S}_{ABCD}=\frac{1}{2}×|AC|×|BD|=\frac{1}{2}$×|$\frac{m}{n+1}$+2|×|$\frac{2n}{m+2}+1$，由此能證明四邊形ABCD的面積為定值2．

解答 解：（1）∵橢圓$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的離心率為$\frac{{\sqrt{3}}}{2}$，過橢圓的焦點(diǎn)且與長軸垂直的弦長為1，
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{2{b}^{2}}{a}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解得a=2，b=1，
∴橢圓C的方程為$\frac{{x}^{2}}{4}+{y}^{2}=1$．
證明：（2）∵橢圓C的方程為$\frac{{x}^{2}}{4}+{y}^{2}$=1，∴A（-2，0），B（0，-1），
設(shè)M（m，n），（m＞0，n＞0），則$\frac{{m}^{2}}{4}+{n}^{2}$=1，即m²+4n²=4，
則直線BM的方程為y=$\frac{n+1}{m}x-1$，
令y=0，得${x}_{C}=\frac{m}{n+1}$，
同理，直線AM的方程為y=$\frac{n}{m+2}（x+2）$，令x=0，得${y}_{D}=\frac{2n}{m+2}$，
∴${S}_{ABCD}=\frac{1}{2}×|AC|×|BD|=\frac{1}{2}$×|$\frac{m}{n+1}$+2|×|$\frac{2n}{m+2}+1$|=$\frac{1}{2}×\frac{（m+2n+2）^{2}}{（m+2）（n+1）}$
=$\frac{1}{2}×\frac{{m}^{2}+4{n}^{2}+4+4mn+4m+8n}{mn+m+2n+2}$=$\frac{1}{2}×\frac{4mn+4m+8n+8}{mn+m+2n+2}$=2，
∴四邊形ABCD的面積為定值2．

點(diǎn)評(píng) 本題考查橢圓方程的求法，考查四邊形的面積為定值的證明，是中檔題，解題時(shí)要認(rèn)真審題，注意橢圓性質(zhì)、韋達(dá)定理、直線與橢圓位置關(guān)系等知識(shí)點(diǎn)的合理運(yùn)用．